0 270084 270092 270098 270102 270108 270110 270114 270120 270122 270128 270134 270138 270140 270144 270150 270152 270158 270162 270164 270168 270170 270174 270176 270178 270179 270180 270182 270183 270184 270186 270188 270192 270194 270198 270200 270204 270210 270212 270218 270222 270224 270228 270234 270240 270242 270248 270252 270254 270260 270264 270270 270278 366461
 D.﹣
D.﹣ 与x轴交于点A(
与x轴交于点A( ,0)、B(4,0)两点,与y轴交于点C.
,0)、B(4,0)两点,与y轴交于点C.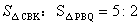 ,求K点坐标.
,求K点坐标.
 秒时,则OP= ,S△ABP= ;
秒时,则OP= ,S△ABP= ;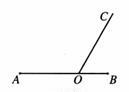


 与
与 轴分别交于点A(-3,0),B(m,0).将y1向右平移4个单位得到y2.
轴分别交于点A(-3,0),B(m,0).将y1向右平移4个单位得到y2. 轴交于点D,与
轴交于点D,与 与图象G有一个公共点,请结合函数图象,求直线
与图象G有一个公共点,请结合函数图象,求直线

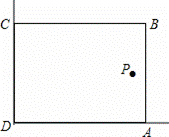
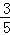 ,求⊙O半径的长.
,求⊙O半径的长.


 ,求AB的长.
,求AB的长.