题目内容
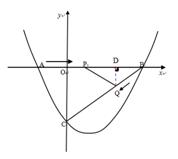
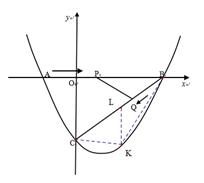
如图,在平面直角坐标系中,抛物线 与x轴交于点A(
与x轴交于点A( ,0)、B(4,0)两点,与y轴交于点C.
,0)、B(4,0)两点,与y轴交于点C.
(1)求抛物线的表达式;
(2)点P从A点出发,在线段AB上以每秒3个单位长度的速度向B点运动,同时点Q从B点出发,在线段BC上以每秒1个单位长度向C点运动.其中一个点到达终点时,另一个点也停止运动.当△PBQ存在时,求运动多少秒使△PBQ的面积最大,最大面积是多少?
(3)当△PBQ的面积最大时,在BC下方的抛物线上存在点K,使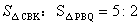 ,求K点坐标.
,求K点坐标.

解:(1)将A(-2,0),B(4,0)两点坐标分别代入y=ax2+bx-3(a≠0),
 即
即 ,…
,…
解得: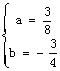
 抛物线的表达式为:
抛物线的表达式为: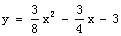
(2)设运动时间为t秒,由题意可知: 
…………………………………… 3分
 过点Q作QD⊥AB,垂直为D,
过点Q作QD⊥AB,垂直为D,
易证△OCB∽△DQB,

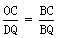
 OC=3,OB=4,BC=5,AP=3t,PB=6-3t,BQ=t,
OC=3,OB=4,BC=5,AP=3t,PB=6-3t,BQ=t,
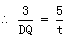
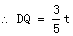


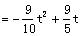
 对称轴
对称轴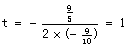
 当运动1秒时,△PBQ面积最大,
当运动1秒时,△PBQ面积最大,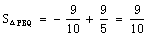 ,最大为
,最大为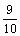 .
.
(3)如图,设K(m,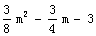 )
)
连接CK、BK,作KL∥y轴交BC与L,
由(2)知: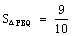 ,
,
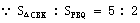

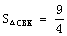
 设直线BC的表达式为y=kx+n
设直线BC的表达式为y=kx+n
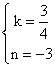
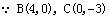
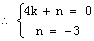 ,解得:
,解得:
 直线BC的表达式为y=
直线BC的表达式为y=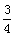 x-3
x-3

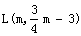
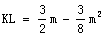

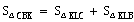

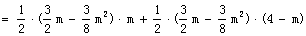
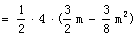
即: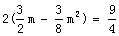
解得: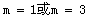
 K坐标为(1,
K坐标为(1,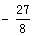 )或(3,
)或(3,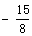 )…
)…

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
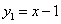 和函数
和函数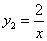 的图象相交于点
的图象相交于点 ,
, 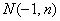 ,若
,若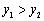 ,则x的取值范围是 。
,则x的取值范围是 。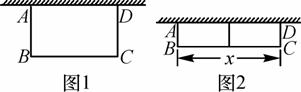
 .
.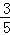 ,求⊙O半径的长.
,求⊙O半径的长.
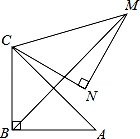
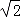 ,将△ABC绕点C逆时针旋转60°,得到△MNC,连接BM,则BM的长是 .
,将△ABC绕点C逆时针旋转60°,得到△MNC,连接BM,则BM的长是 .