题目内容
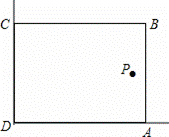
在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两边足够长),用28m长的篱笆围成一个矩形花园ABCD(篱笆只围AB,BC两边),设AB=xm.
(1)若花园的面积为192m2,求x的值;
(2)若在P处有一棵树与墙CD,AD的距离分别是15m和6m,要将这棵树围在花园内(含边界,不考虑树的粗细),求x取何值时,花园面积S最大,并求出花园面积S的最大值.
解:(1)∵AB=xm,则BC=(28﹣x)m,
∴x(28﹣x)=192,
解得:x1=12,x2=16,
答:x的值为12m或16m;……………………… 2分
(2)由题意可得出: ,………………… 3分
,………………… 3分
解得: .
.
又S=x(28﹣x)=﹣x2+28x=﹣(x﹣14)2+196,
∴当x≤14时,S随x的增大而增大.
∴x=13时,S取到最大值为:S=﹣(13﹣14)2+196=195.……………………… 5分
答:x为13m时,花园面积S最大,最大面积为195m2.

练习册系列答案
相关题目
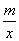 的图象交于
的图象交于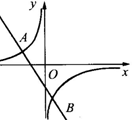

 的图象相交于A,B两点,点B的坐标为(2m,-m).
的图象相交于A,B两点,点B的坐标为(2m,-m).
 D.﹣
D.﹣