题目内容
已知如图,在△ABC中,∠A=30°,∠C=105°,AC= ,求AB的长.
,求AB的长.

 解:在△ABC中,∠A=30°,∠C=105°
解:在△ABC中,∠A=30°,∠C=105°
∴∠B=45°,
过C作CD⊥AB于D,
∴∠ADC=∠BDC=90°,
∵∠B=45°,
∴∠BCD=∠B=45°,
∴CD=BD,
∵∠A=30°,AC=2 ,
,
∴CD= ,
,
∴BD=CD= ,
,
由勾股定理得:AD= =3,
=3,
∴AB=AD+BD=3+ .
.

练习册系列答案
相关题目
已知二次函数y=ax2+bx+c中,其函数y与自变量x之间的部分对应值如下表所示:
| x | … | 0 | 1 | 2 | 3 | … |
| y | … | 5 | 2 | 1 | 2 | … |
点A(x1,y1)、B(x2,y2)在函数的图象上,则当0<x1<1,2<x2<3时,y1与y2的大小关系正确的是( )
A.y1≥y2 B.y1>y2 C.y1<y2 D.y1≤y2
 B.c=
B.c=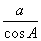 C.c=
C.c=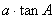 D.c=
D.c=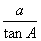
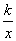 的图象上,AB垂直于x轴,
的图象上,AB垂直于x轴,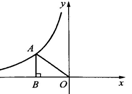

 明明对首都博物馆建筑物产生了浓厚的兴趣,站到首都博物馆北广场,他被眼前这座建筑物震撼了.整个建筑宏大壮观,斜出的青铜展馆和北墙面交出一条抛物线,抛物线与外立面之间和谐、统一,明明走到过街天桥上照了一张照片(如图所示).明明想了想,算了算,对旁边的文文说:“我猜想这条抛物线的顶点到地面的距离应是15.7米左右.” 文文反问:“你猜想的理由是什么”?明明说:“我的理由是 ”. 明明又说:“不过这只是我的猜想,这次准备不充分,下次来我要用学过的数学知识准确的测测这个高度,我想用学到的 知识, 我要带 等测量工具”.
明明对首都博物馆建筑物产生了浓厚的兴趣,站到首都博物馆北广场,他被眼前这座建筑物震撼了.整个建筑宏大壮观,斜出的青铜展馆和北墙面交出一条抛物线,抛物线与外立面之间和谐、统一,明明走到过街天桥上照了一张照片(如图所示).明明想了想,算了算,对旁边的文文说:“我猜想这条抛物线的顶点到地面的距离应是15.7米左右.” 文文反问:“你猜想的理由是什么”?明明说:“我的理由是 ”. 明明又说:“不过这只是我的猜想,这次准备不充分,下次来我要用学过的数学知识准确的测测这个高度,我想用学到的 知识, 我要带 等测量工具”.