题目内容
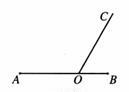
如图1,点O在线段AB上,AO=2,OB=1,OC为射线,且∠BOC=60°,动点P以每秒2个单位长度的速度从点O出发,沿射线OC做匀速运动,设运动时间为t秒.
(1)当t= 秒时,则OP= ,S△ABP= ;
秒时,则OP= ,S△ABP= ;
(2)当△ABP是直角三角形时,求t的值;
(3)如图2,当AP=AB时,过点A作AQ∥BP,并使得∠QOP=∠B,求证:AQ·BP=3.为了证明AQ·BP=3,小华同学尝试过O点作OE∥AP交BP于点E.试利用小华同学给我们的启发补全图形并证明AQ·BP=3.
| |||||
| |||||
| |||||


.解:(1)1, ;…………………………………… 2分
;…………………………………… 2分
(2)①∵∠A<∠BOC=60°,
∴∠A不可能是直角.

 ②当∠ABP=90°时,
②当∠ABP=90°时,
∵∠BOC=60°,
∴∠OPB=30°.
∴OP=2OB,即2t=2.
∴t=1. …………………………………… 3分
③当∠APB=90°,如图,过点P作PD⊥AB于点D,则OP=2t,OD=t,PD= ,AD=
,AD= ,DB=
,DB= .
.
∵∠APD+∠BPD=90°,∠B+∠BPD=90°,∴∠APD=∠B. ∴△APD∽△PBD.
∴ ,即
,即 ,即
,即 ,解得
,解得 (舍去).
(舍去).
…………………………………… 4分
(3)补全图形,如图
∵AP=AB,
∴∠APB=∠B.
∵OE∥AP
∴∠OEB=∠APB=∠B.
∵AQ∥BP,
∴∠QAB+∠B=180°.
又∵∠3+∠OEB=180°,
∴∠3=∠QAB.
又∵∠AOC=∠2+∠B=∠1+∠QOP,
∵∠B=∠QOP,
∴∠1=∠2.
∴△QAO∽△OEP.
 ∴
∴ ,即AQ·EP=EO·AO.
,即AQ·EP=EO·AO.
∵OE∥AP,
∴△OBE∽△ABP.
∴ .
.
∴OE= AP=1,BP=
AP=1,BP= EP.
EP.
∴AQ·BP=AQ· EP=
EP= AO·OE=
AO·OE= ×2×1=3. …………………………………… 6分
×2×1=3. …………………………………… 6分

 明明对首都博物馆建筑物产生了浓厚的兴趣,站到首都博物馆北广场,他被眼前这座建筑物震撼了.整个建筑宏大壮观,斜出的青铜展馆和北墙面交出一条抛物线,抛物线与外立面之间和谐、统一,明明走到过街天桥上照了一张照片(如图所示).明明想了想,算了算,对旁边的文文说:“我猜想这条抛物线的顶点到地面的距离应是15.7米左右.” 文文反问:“你猜想的理由是什么”?明明说:“我的理由是 ”. 明明又说:“不过这只是我的猜想,这次准备不充分,下次来我要用学过的数学知识准确的测测这个高度,我想用学到的 知识, 我要带 等测量工具”.
明明对首都博物馆建筑物产生了浓厚的兴趣,站到首都博物馆北广场,他被眼前这座建筑物震撼了.整个建筑宏大壮观,斜出的青铜展馆和北墙面交出一条抛物线,抛物线与外立面之间和谐、统一,明明走到过街天桥上照了一张照片(如图所示).明明想了想,算了算,对旁边的文文说:“我猜想这条抛物线的顶点到地面的距离应是15.7米左右.” 文文反问:“你猜想的理由是什么”?明明说:“我的理由是 ”. 明明又说:“不过这只是我的猜想,这次准备不充分,下次来我要用学过的数学知识准确的测测这个高度,我想用学到的 知识, 我要带 等测量工具”.