0 257440 257448 257454 257458 257464 257466 257470 257476 257478 257484 257490 257494 257496 257500 257506 257508 257514 257518 257520 257524 257526 257530 257532 257534 257535 257536 257538 257539 257540 257542 257544 257548 257550 257554 257556 257560 257566 257568 257574 257578 257580 257584 257590 257596 257598 257604 257608 257610 257616 257620 257626 257634 366461
 如图,有三条线段AB、BD、DC,AB=6,BD=8,DC=2,且AB∥DC.点E和点F分别为BD上的两个动点,且
如图,有三条线段AB、BD、DC,AB=6,BD=8,DC=2,且AB∥DC.点E和点F分别为BD上的两个动点,且 如图,以△ABC的三边为边在BC的同一侧分别作三个等边三角形,即△ABD、△BCE、△ACF为等边三角形.请回答下列问题:
如图,以△ABC的三边为边在BC的同一侧分别作三个等边三角形,即△ABD、△BCE、△ACF为等边三角形.请回答下列问题: 如图所示,有一等腰三角形钢板,其腰AB=40cm,底边BC为48cm,求这个钢板零件的面积.
如图所示,有一等腰三角形钢板,其腰AB=40cm,底边BC为48cm,求这个钢板零件的面积.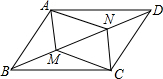 如图,M、N是平行四边形ABCD对角线BD上两点.
如图,M、N是平行四边形ABCD对角线BD上两点. 已知平面直角坐标系xOy(如图),直线y=
已知平面直角坐标系xOy(如图),直线y=