题目内容
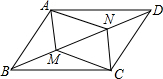 如图,M、N是平行四边形ABCD对角线BD上两点.
如图,M、N是平行四边形ABCD对角线BD上两点.(1)若BM=MN=DN,求证:四边形AMCN为平行四边形;
(2)若M、N为对角线BD上的动点(均可与端点重合),设BD=12cm,点M由点B向点D匀速运动,速度为2(cm/s),同时点N由点D向点B匀速运动,速度为a(cm/s),运动时间为t(s).若要使四边形AMCN为平行四边形,求a的值及t的取值范围.
考点:平行四边形的判定与性质
专题:动点型
分析:(1)首先连解AC,AC交BD于O,易证得AC、MN互相平分;即可判定四边形AMCN为平行四边形;
(2)由要使四边形AMCN为平行四边形,即OM=ON,可得a=2;又由当M、M重合于点O,即t=
=
=3时,则点A、M、C、N在同一直线上,不能组成四边形,且当点M由A运动到点D时,t=12÷2=6,即可求得答案.
(2)由要使四边形AMCN为平行四边形,即OM=ON,可得a=2;又由当M、M重合于点O,即t=
| BD |
| a+2 |
| 12 |
| 4 |
解答: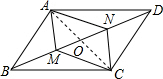 (1)证明:连接AC,交BD于点O,
(1)证明:连接AC,交BD于点O,
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵BM=DN,
∴OB-BM=OD-DN,
∴OM=ON,
∴四边形AMCN为平行四边形;
(2)解:要使四边形AMCN为平行四边形,即OM=ON,
∴a=2;
∵当M、M重合于点O,即t=
=
=3时,则点A、M、C、N在同一直线上,不能组成四边形,且当点M由A运动到点D时,t=12÷2=6,
∴当0≤t<3或3<t≤6时,四边形AMCN为平行四边形.
 (1)证明:连接AC,交BD于点O,
(1)证明:连接AC,交BD于点O,∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵BM=DN,
∴OB-BM=OD-DN,
∴OM=ON,
∴四边形AMCN为平行四边形;
(2)解:要使四边形AMCN为平行四边形,即OM=ON,
∴a=2;
∵当M、M重合于点O,即t=
| BD |
| a+2 |
| 12 |
| 4 |
∴当0≤t<3或3<t≤6时,四边形AMCN为平行四边形.
点评:此题考查了平行四边形的性质与判定.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想的应用.

练习册系列答案
 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
在根式
,
,
,
,
中最简二次根式的个数是 ( )
| 3 |
| x2+6x+9 |
| a2+b2 |
| (x+y)(x2-y2) |
|
| A、2个 | B、3个 | C、4个 | D、5个 |
 已知:如图,菱形ABCD中,对角线AC与BD相交于点O,OE∥DC交BC于点E,AC=6,BD=8,则OE的长为
已知:如图,菱形ABCD中,对角线AC与BD相交于点O,OE∥DC交BC于点E,AC=6,BD=8,则OE的长为 如图,已知抛物线y=-x2-3x+m经过点C(-2,6),与x轴相交于A、B两点(A在B的左侧),与y轴交于点D.
如图,已知抛物线y=-x2-3x+m经过点C(-2,6),与x轴相交于A、B两点(A在B的左侧),与y轴交于点D. 如图所示,有一等腰三角形钢板,其腰AB=40cm,底边BC为48cm,求这个钢板零件的面积.
如图所示,有一等腰三角形钢板,其腰AB=40cm,底边BC为48cm,求这个钢板零件的面积.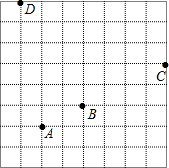 如图,是一个规格为8×8的球桌,小明用A球撞击B球,到C处反弹,再撞击桌边D处,请选择适当的平面直角坐标系,并用坐标表示各点的位置.
如图,是一个规格为8×8的球桌,小明用A球撞击B球,到C处反弹,再撞击桌边D处,请选择适当的平面直角坐标系,并用坐标表示各点的位置. 如图,抛物线y=x2沿直线y=x向上平移
如图,抛物线y=x2沿直线y=x向上平移