题目内容
 如图,有三条线段AB、BD、DC,AB=6,BD=8,DC=2,且AB∥DC.点E和点F分别为BD上的两个动点,且
如图,有三条线段AB、BD、DC,AB=6,BD=8,DC=2,且AB∥DC.点E和点F分别为BD上的两个动点,且| DF |
| BE |
| 1 |
| 3 |
(1)求证:△ABE∽△CDF;
(2)当EF=2时,求BE的长度;
(3)在以上2个问题的解题过程中,概括(或者描述)你所用到数学基本知识(定义、定理等)或者是利用的数学思想方法.(共写出2点即可)
考点:相似三角形的判定与性质
专题:
分析:(1)由“SAS”可以判定∴△ABE∽△CDF.
(2)设BE=x,则DF=
x,又∵BD=8,∴x+
x=8-2,解方程即可得到答案.
(3)本题用到的数学基本知识较多,如:①两直线平行,内错角相等; ②相似三角形对应边成比例;③两边对应成比例,且夹角相等的两个三角形相似
;④分类讨论思想;⑤数形结合思想….
(2)设BE=x,则DF=
| 1 |
| 3 |
| 1 |
| 3 |
(3)本题用到的数学基本知识较多,如:①两直线平行,内错角相等; ②相似三角形对应边成比例;③两边对应成比例,且夹角相等的两个三角形相似
;④分类讨论思想;⑤数形结合思想….
解答:(1)证明:∵AB∥CD∴∠B=∠D,
又∵
=
,
=
,
∴△ABE∽△CDF.
(2)解:设BE=x,则DF=
x,
又∵BD=8,
∴x+
x=8-2,
解得:x=
,
∴BE的长度为:
.
(3)解:①两直线平行,内错角相等
②相似三角形对应边成比例
③两边对应成比例,且夹角相等的两个三角形相似
④分类讨论思想
⑤数形结合思想
⑥方程思想(列方程解决实际问题).
又∵
| CD |
| AB |
| 1 |
| 3 |
| DE |
| BE |
| 1 |
| 3 |
∴△ABE∽△CDF.
(2)解:设BE=x,则DF=
| 1 |
| 3 |
又∵BD=8,
∴x+
| 1 |
| 3 |
解得:x=
| 9 |
| 2 |
∴BE的长度为:
| 9 |
| 2 |
(3)解:①两直线平行,内错角相等
②相似三角形对应边成比例
③两边对应成比例,且夹角相等的两个三角形相似
④分类讨论思想
⑤数形结合思想
⑥方程思想(列方程解决实际问题).
点评:本题主要考查了三角形形相似的判定以及线段长度的求法,解答本题的关键是学会用方程思想求线段的长度.

练习册系列答案
相关题目
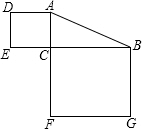 如图,在Rt△ABC中,∠C=90°,若AB=13,则正方形ACED和正方形BCFG的面积和为( )
如图,在Rt△ABC中,∠C=90°,若AB=13,则正方形ACED和正方形BCFG的面积和为( )| A、150 | B、169 |
| C、225 | D、无法计算 |
 已知:如图,反比例函数y=
已知:如图,反比例函数y=