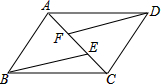如图，已知点A、F、E、C在同一直线上，AB∥CD，∠ABE=∠CDF，AF=CE．
（1）从图中任找两组全等三角形；
（2）从（1）中任选一组进行证明．

若a+b=5，ab=2，求（a+b）⁴，（a+b）⁸的值．

先化简，再求值．（a+b）（a-b）+b（a+2b）-b²，其中a=1，b=-2．

已知α、β是关于x的一元二次方程x²+（m-2）x+1=0的两个实数根，求（1+mα+α²）（1+mβ+β²）的值．

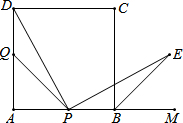如图1，正方形ABCD的边长为6，点P、Q分别是AB、AD边上的动点，且AP=AQ，点M在AB的延长线上，BE平分∠CBM，PD⊥PE．
（1）求证：PD=PE；
（2）当AP的长为多少时，△PDQ的面积最大，并求出面积最大值．

如图，用红、蓝两种颜色随机地对A、B、C三个区域分别进行涂色，每个区域必须涂色并且只能涂一种颜色，请用列举法（画树状图或列表）求A、C两个区域所涂颜色不相同的概率．

如图，在△ABC中，AB=AC，BD=CD，DE⊥AB，DF⊥AC，垂足分别为点E、F．
求证：△BED≌△CFD．

实验与探究：
三角点阵前n行的点数计算
如图是一个三角点阵，从上向下数有无数多行，其中第一行有1个点，第二行有2个点…第n行有n个点…
容易发现，10是三角点阵中前4行的点数的和，你能发现300是前多少行的点数的和吗？
如果要用试验的方法，由上而下地逐行的相加其点数，虽然你能发现1+2+3+4+…+23+24=300．得知300是前24行的点数的和，但是这样寻找答案需我们先探求三角点阵中前n行的点数的和与n的数量关系
前n行的点数的和是1+2+3+…+（n-2）+（n-1）+n，可以发现．
2×[1+2+3+…+（n-2）+（n-1）+n]
=[1+2+3+…+（n-2）+（n-1）+n]+[n+（n-1）+（n-2）+…3+2+1]
把两个中括号中的第一项相加，第二项相加…第n项相加，上式等号的后边变形为这n个小括号都等于n+1，整个式子等于n（n+1），于是得到
1+2+3+…+（n-2）+（n-1）+n=

1

2

n（n+1）
这就是说，三角点阵中前n项的点数的和是

1

2

n（n+1）
下列用一元二次方程解决上述问题
设三角点阵中前n行的点数的和为300，则有

1

2

n（n+1）=300
整理这个方程，得：n²+n-600=0
解方程得：n₁=24，n₂=-25
根据问题中未知数的意义确定n=24，即三角点阵中前24行的点数的和是300．
请你根据上述材料回答下列问题：
（1）三角点阵中前n行的点数的和能是600吗？如果能，求出n；如果不能，试用一元二次方程说明道理．
（2）如果把图中的三角点阵中各行的点数依次换成2、4、6、…、2n、…，你能探究出前n行的点数的和满足什么规律吗？这个三角点阵中前n行的点数的和能是600吗？如果能，求出n；如果不能，试用一元二次方程说明道理．

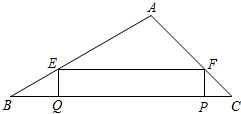如图，在△ABC中，AB=20cm，AC=10 

2

cm，∠C=45°，在线段BA上，动点E以每秒2cm的速度从点B出发向点A做匀速运动，在线段CA上，动点F从点C出发向点A做匀速运动，速度为每秒acm，当点E、F其中一点停止运动时，另一点也停止运动，分别过点E、F作BC的垂线，垂足为Q、P，连接EF．若点E、F同时运动，运动时间为t秒，在运动过程中四边形EFPQ总为矩形（点E、F重合除外）．
（1）求a的值；
（2）当t为多少时，矩形EFPQ为正方形；
（3）当t为多少时，矩形EFPQ的面积S最大？并求出最大值．（以上结果保留根号）

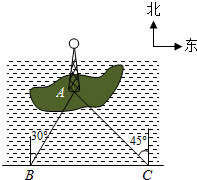如图，湖中的小岛上有一标志性建筑物，其底部为A，某人在岸边的B处测得A在B的北偏东30°的方向上，然后沿岸边直行4公里到达C处，再次测得A在C的北偏西45°的方向上（其中A、B、C在同一平面上）．求这个标志性建筑物底部A到岸边BC的最短距离．