题目内容
已知α、β是关于x的一元二次方程x2+（m-2）x+1=0的两个实数根，求（1+mα+α2）（1+mβ+β2）的值．
考点：根与系数的关系,一元二次方程的解
专题：计算题
分析：先根据一元二次方程的解的定义得到α2+（m-2）α+1=0，β2+（m-2）β+1=0，变形得到α2+mα+1=2α，β2+mβ+1=2β，则（1+mα+α2）（1+mβ+β2）可变形为4αβ，然后利用根与系数的关系得到αβ=1，再利用整体代入的方法计算即可．
解答：解：∵α、β是关于x的一元二次方程x2+（m-2）x+1=0的两个实数根，
∴α2+（m-2）α+1=0，β2+（m-2）β+1=0，即α2+mα+1=2α，β2+mβ+1=2β，
∴（1+mα+α2）（1+mβ+β2）=2α•2β=4αβ，
∵α、β是关于x的一元二次方程x2+（m-2）x+1=0的两个实数根，
∴αβ=1，
∴（1+mα+α2）（1+mβ+β2）=4αβ=4×1=4．
∴α2+（m-2）α+1=0，β2+（m-2）β+1=0，即α2+mα+1=2α，β2+mβ+1=2β，
∴（1+mα+α2）（1+mβ+β2）=2α•2β=4αβ，
∵α、β是关于x的一元二次方程x2+（m-2）x+1=0的两个实数根，
∴αβ=1，
∴（1+mα+α2）（1+mβ+β2）=4αβ=4×1=4．
点评：本题考查了一元二次方程ax2+bx+c=0（a≠0）的根与系数的关系：若方程两个为x1，x2，则x1+x2=-
，x1•x2=
．也考查了一元二次方程的解．
| b |
| a |
| c |
| a |
练习册系列答案
应用题天天练四川大学出版社系列答案
相关题目
已知直角三角形两边的长为3和4，则第三边的长为（ ）
| A、5 | ||
B、
| ||
| C、5或-1 | ||
| D、以上都不对 |
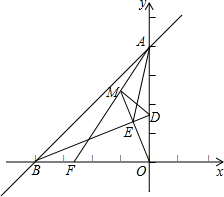在直线y=x+4与坐标轴交于A、B两点，BD平分∠ABO，交y轴于D，OE⊥BD交AB于E点，点F在OB上，且OF=AE，AF与OE相交于M点．求证：
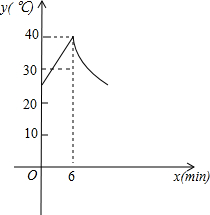墨墨在妈妈生日当天购买了一个足浴盆作为生日礼物送给妈妈．墨墨妈妈在使用该足浴盆泡脚时，最初注入的水的温度是25℃，加热6min后，水温达到最高温度40℃，然后该足浴盆自动停止加热进行保温，设定保温过程中，水温的最低温度不低于30℃，当水温降至30℃时，该足浴盆又会再次自动加热，以此循环．加热时，温度y（℃）与时间x（min）成一次函数关系；保温时，温度y（℃）与时间x（min）成反比例函数关系，第一个加热和保温过程如图所示． 
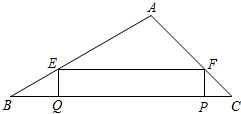如图，在△ABC中，AB=20cm，AC=10 
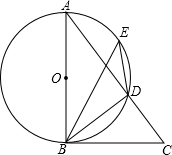如图，AB是⊙O的直径，点E是
有六张完全相同的卡片，分A，B两组，每组三张，在A组的卡片上分别画上“√，×，√”，在B组的卡片上分别画上“√，×，×”，如图1所示．