题目内容
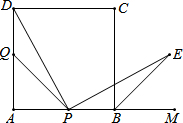 如图1,正方形ABCD的边长为6,点P、Q分别是AB、AD边上的动点,且AP=AQ,点M在AB的延长线上,BE平分∠CBM,PD⊥PE.
如图1,正方形ABCD的边长为6,点P、Q分别是AB、AD边上的动点,且AP=AQ,点M在AB的延长线上,BE平分∠CBM,PD⊥PE.(1)求证:PD=PE;
(2)当AP的长为多少时,△PDQ的面积最大,并求出面积最大值.
考点:正方形的性质,全等三角形的判定与性质
专题:
分析:(1)判断出△APQ是等腰直角三角形,然后求出∠DQP=135°,再求出∠PBE=135°,从而得到∠DQP=∠PBE,再求出DQ=PB,根据同角的余角相等求出∠ADP=∠BPE,然后利用“角边角”证明△DPQ和△PEB全等,根据全等三角形对应边相等可得PD=PE;
(2)设AP=x,表示出DQ,然后根据三角形的面积公式列式并整理,再根据二次函数的最值问题解答.
(2)设AP=x,表示出DQ,然后根据三角形的面积公式列式并整理,再根据二次函数的最值问题解答.
解答:(1)证明:∵AP=AQ,∠A=90°,
∴△APQ是等腰直角三角形,
∴∠AQP=45°,
∴∠DQP=135°,
∵BE平分∠CBM,
∴∠CBE=
×90°=45°,
∴∠PBE=135°,
∴∠DQP=∠PBE,
∵AP=AQ,AB=AD,
∴AB-AP=AD-AQ,
即DQ=PB,
∵PD⊥PE,
∴∠APD+∠BPE=90°,
又∵∠APD+∠ADP=90°,
∴∠ADP=∠BPE,
在△DPQ和△PEB中,
,
∴△DPQ≌△PEB(ASA),
∴PD=PE;
(2)解:设AP=x,则DQ=PB=6-x,
△PDQ的面积=
DQ•AP=
(6-x)•x=-
(x-3)2+
,
∵a=-
<0,
∴当x=3,即AP=3时,△PDQ的面积最大,最大值为
.
∴△APQ是等腰直角三角形,
∴∠AQP=45°,
∴∠DQP=135°,
∵BE平分∠CBM,
∴∠CBE=
| 1 |
| 2 |
∴∠PBE=135°,
∴∠DQP=∠PBE,
∵AP=AQ,AB=AD,
∴AB-AP=AD-AQ,
即DQ=PB,
∵PD⊥PE,
∴∠APD+∠BPE=90°,
又∵∠APD+∠ADP=90°,
∴∠ADP=∠BPE,
在△DPQ和△PEB中,
|
∴△DPQ≌△PEB(ASA),
∴PD=PE;
(2)解:设AP=x,则DQ=PB=6-x,
△PDQ的面积=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 9 |
| 2 |
∵a=-
| 1 |
| 2 |
∴当x=3,即AP=3时,△PDQ的面积最大,最大值为
| 9 |
| 2 |
点评:本题考查了正方形的性质,角平分线的定义,全等三角形的判定与性质,二次函数的最值问题,熟记性质并准确识图确定出全等三角形和全等的条件是解题的关键.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
下列说法正确的是( )
| A、一元二次方程的一般形式是ax2+bx+c=0 | ||||
| B、方程x2=x的解是x=1 | ||||
C、一元二次方程的一般形式是ax2+bx+c=0 的根是x=
| ||||
| D、方程x(x+2)(x-3)=0的实数根有三个 |
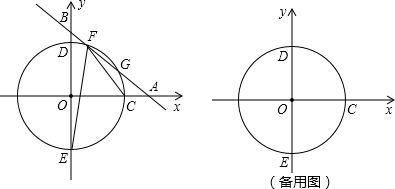
 如图,直线L:y=-x+3与两坐标轴分别相交于点A、B.
如图,直线L:y=-x+3与两坐标轴分别相交于点A、B.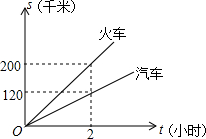 已知A、B两地的路程为240千米,某经销商每天都要用汽车或火车将x吨保鲜品一次性由A地运往B地,受各种因素限制,下一周只能采用汽车和火车中的一种进行运输,且须提前预订,现有货运收费项目及收费标准表、行驶路程s(千米)与行驶时间t(时间)的函数图象,如图.
已知A、B两地的路程为240千米,某经销商每天都要用汽车或火车将x吨保鲜品一次性由A地运往B地,受各种因素限制,下一周只能采用汽车和火车中的一种进行运输,且须提前预订,现有货运收费项目及收费标准表、行驶路程s(千米)与行驶时间t(时间)的函数图象,如图.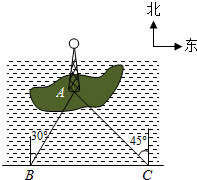 如图,湖中的小岛上有一标志性建筑物,其底部为A,某人在岸边的B处测得A在B的北偏东30°的方向上,然后沿岸边直行4公里到达C处,再次测得A在C的北偏西45°的方向上(其中A、B、C在同一平面上).求这个标志性建筑物底部A到岸边BC的最短距离.
如图,湖中的小岛上有一标志性建筑物,其底部为A,某人在岸边的B处测得A在B的北偏东30°的方向上,然后沿岸边直行4公里到达C处,再次测得A在C的北偏西45°的方向上(其中A、B、C在同一平面上).求这个标志性建筑物底部A到岸边BC的最短距离.