如图，A、P、B、C是⊙O上四点，且∠APC=∠CPB=60?．连接CP、BP、AP，
如图，已知AB是⊙O的直径，C是上半圆上异于A、B的点，CD平分∠ACB，交⊙O于点D，连接BD，若∠A=30°，BC=1，求AC、BD的长．
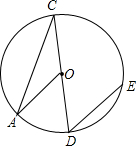
如图，CD为⊙O的直径，过点D的弦DE平行于半径OA，若∠D的度数是50°，则∠A的度数为（ ）| A、50° | B、40° |
| C、30° | D、25° |
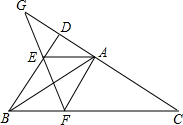在△ABC中，以边AB为轴翻折∠ABC，使翻折后BC的对应边交CA的延长线于点D．分别过A作AE∥BC交BD于E，作AF∥BD交BC于F，延长CD、EF交于G．若BC=2BD，BE=1，求DE的长
如图所示是某酒店门前的台阶，现该酒店经理要在台阶上铺上一块红地毯，问这块红地毯至少要多大？
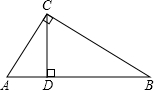如图，在△ABC中，∠ACB=90°，CD⊥AB于点D，若AC=2| 3 |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
如图，CD为⊙O的直径，过点D的弦DE平行于半径OA，若∠D的度数是50°，则∠A的度数为（ ）在△ABC中，以边AB为轴翻折∠ABC，使翻折后BC的对应边交CA的延长线于点D．分别过A作AE∥BC交BD于E，作AF∥BD交BC于F，延长CD、EF交于G．若BC=2BD，BE=1，求DE的长如图，在△ABC中，∠ACB=90°，CD⊥AB于点D，若AC=2
如图所示的正方形网格中，△ABC的顶点均在格点上，在所给平面直角坐标系中解答下列问题：
如图，方格纸中的每个小方格都是边长为1个单位的正方形，建立如图所示的平面直角坐标系，△ABC的顶点均在格点上，点B的坐标为（1，0）
如图，△ABC经过旋转后到△A′B′C′位置，
如图，方格纸中的每个小方格都是边长为1个单位的正方形，在建立平面直角坐标系后，△ABC的顶点均在格上，点C的坐标为（4，-1），