题目内容
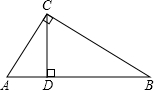 如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,若AC=2
如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,若AC=2| 3 |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:解直角三角形
专题:
分析:先根据勾股定理求得BC的长度,然后根据CD⊥AB得出∠BCD=∠A,继而可求得tan∠BCD的值.
解答:解:∵在△ABC中,∠ACB=90°,AC=2
,AB=4
,
∴BC=
=2
,
∵CD⊥AB,
∴∠BCD+∠B=90°,
∵∠A+∠B=90°,
∴∠BCD=∠A,
则tan∠BCD=tan∠A=
=
=
.
故选D.
| 3 |
| 2 |
∴BC=
| AB2-AC2 |
| 5 |
∵CD⊥AB,
∴∠BCD+∠B=90°,
∵∠A+∠B=90°,
∴∠BCD=∠A,
则tan∠BCD=tan∠A=
| BC |
| AC |
2
| ||
2
|
| ||
| 3 |
故选D.
点评:本题考查解直角三角形,勾股定理,锐角三角函数的定义及运用:在直角三角形中,锐角的正弦为对边比斜边,余弦为邻边比斜边,正切为对边比邻边.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
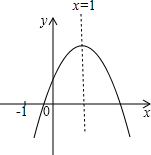 已知二次函数y=ax2+bx+c的图象如图所示,下列结论:
已知二次函数y=ax2+bx+c的图象如图所示,下列结论:①abc>0;②a+c>b;③4a+2b+c>0;④2a+b=0;⑤b2-4ac>0
其中正确的结论有( )
| A、2个 | B、3个 | C、4个 | D、5个 |
AD是△ABC的角平分线,作DE⊥AB于E,DF⊥AC于F,下列结论错误的是( )
| A、DE=DF |
| B、AE=AF |
| C、BD=CD |
| D、∠ADE=∠ADF |
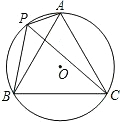 如图,A、P、B、C是⊙O上四点,且∠APC=∠CPB=60?.连接CP、BP、AP,
如图,A、P、B、C是⊙O上四点,且∠APC=∠CPB=60?.连接CP、BP、AP,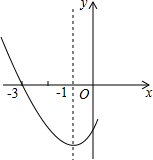 如图是二次函数y=ax2+bx+c图象的一部分,其对称轴是x=-1,且过点(-3,0),下列说法:①abc<0;②2a-b=0;③4a+2b+c<0;④若(-5,y1),(
如图是二次函数y=ax2+bx+c图象的一部分,其对称轴是x=-1,且过点(-3,0),下列说法:①abc<0;②2a-b=0;③4a+2b+c<0;④若(-5,y1),(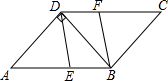 如图,在平行四边形ABCD中,∠A=60°,AD=6,且AD⊥BD,点E,F分别是边AB,CD上的动点,且AE=CF.
如图,在平行四边形ABCD中,∠A=60°,AD=6,且AD⊥BD,点E,F分别是边AB,CD上的动点,且AE=CF.