如图，等边△ABC的边长为8，点O为边AC的四等分点（AO＜CO），点P为边AB上一动点，连接OP．将△AOP绕点O逆时针旋转，得到△A′OP′，且使得点A′落在边AB上，当点P′落在边BC上时，则AP的长为
如图，4×4方格中每个小正方形的边长都为1．
如图，数轴上点A，B对应的数分别为1，| 7 |
A、
| ||
B、
| ||
C、1-
| ||
D、2-
|
在-2，-
，-3
，-π这四个数中，最大的数是（ ）
| 3 |
| 1 |
| 3 |
| A、-2 | ||
B、-
| ||
C、-3
| ||
| D、-π |
如图：在平面直角坐标系中，A（-2，0），B（0，1），有一组抛物线Ln，它们的顶点Cn（Xn，Yn）在直线AB上，并且经过点（Xn+1，0），当n=1，2，3，4，5…时，Xn=2，3，5，8，13…，根据上述规律，写出抛物线L1的表达式为
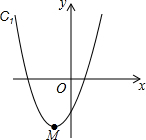如图所示，已知抛物线C1：y=x2+2x-1的顶点为M，抛物线C2与抛物线C1关于x轴对称，将抛物线C2向右平移得到抛物线C3，C3的顶点为N，且点M、N关于原点成中心对称，则抛物线C3的解析式为如图，数轴上点A，B对应的数分别为1，如图所示，已知抛物线C1：y=x2+2x-1的顶点为M，抛物线C2与抛物线C1关于x轴对称，将抛物线C2向右平移得到抛物线C3，C3的顶点为N，且点M、N关于原点成中心对称，则抛物线C3的解析式为