题目内容
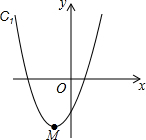 如图所示,已知抛物线C1:y=x2+2x-1的顶点为M,抛物线C2与抛物线C1关于x轴对称,将抛物线C2向右平移得到抛物线C3,C3的顶点为N,且点M、N关于原点成中心对称,则抛物线C3的解析式为
如图所示,已知抛物线C1:y=x2+2x-1的顶点为M,抛物线C2与抛物线C1关于x轴对称,将抛物线C2向右平移得到抛物线C3,C3的顶点为N,且点M、N关于原点成中心对称,则抛物线C3的解析式为考点:二次函数图象与几何变换
专题:
分析:根据抛物线y=x2+2x-1可以求得顶点为M(1,0),则点N(-1,0).由题意知,抛物线C1与抛物线C3关于原点对称.
解答:解:∵抛物线y=x2+2x-1=(x-1)2,
∴M(1,0),
又∵点M、N关于原点成中心对称,
∴N(-1,0).
∵点M、N关于原点成中心对称,
∴抛物线C1与抛物线C3关于原点对称,
∴抛物线C3的解析式为 y=-x2+2x+1.
故答案是:y=-x2+2x+1.
∴M(1,0),
又∵点M、N关于原点成中心对称,
∴N(-1,0).
∵点M、N关于原点成中心对称,
∴抛物线C1与抛物线C3关于原点对称,
∴抛物线C3的解析式为 y=-x2+2x+1.
故答案是:y=-x2+2x+1.
点评:本题主要考查了讨论两个二次函数的图象的平移问题,只需看顶点坐标是如何平移得到的即可,关于x轴对称的两条抛物线的顶点的横坐标相等,纵坐标互为相反数,二次项系数互为相反数,难度适中.

练习册系列答案
相关题目
实数
,0,-π,
,0.2020020002…,
,其中无理数的个数是( )
| 3 | 27 |
| 1 |
| 3 |
| 2 |
| A、1个 | B、2个 | C、3个 | D、4个 |
 如图,在矩形纸片ABCD中,AB=5CM,BC=10CM,CD上有一点E,ED=2CM,AD上有一点P,PD=3CM,过点P作PF⊥AD,交BC于点F,将纸片折叠,使点P与点E重合,折痕与PF交于点Q,则PQ的长是( )
如图,在矩形纸片ABCD中,AB=5CM,BC=10CM,CD上有一点E,ED=2CM,AD上有一点P,PD=3CM,过点P作PF⊥AD,交BC于点F,将纸片折叠,使点P与点E重合,折痕与PF交于点Q,则PQ的长是( )A、
| ||
| B、3cm | ||
| C、2cm | ||
D、
|
 如图,数轴上点A,B对应的数分别为1,
如图,数轴上点A,B对应的数分别为1,| 7 |
A、
| ||
B、
| ||
C、1-
| ||
D、2-
|
 如图,延长线段AB到C,使BD=3AB,点D是线段BC的中点,CD=6,求线段AC的长.
如图,延长线段AB到C,使BD=3AB,点D是线段BC的中点,CD=6,求线段AC的长.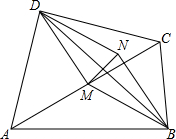 已知如图,四边形ABCD中,∠ABC=∠ADC=90°,M是AC中点,MN⊥BD且与MD的平行线BN相交于N.
已知如图,四边形ABCD中,∠ABC=∠ADC=90°,M是AC中点,MN⊥BD且与MD的平行线BN相交于N.