若抛物线y=x2-4x+3-t(t为实数)在0<x<3
的范围内与x轴有公共点,则t的取值范围为( )
| 1 |
| 2 |
| A、-1<t<3 | ||
| B、-1≤t<3 | ||
C、
| ||
| D、t≥-1 |
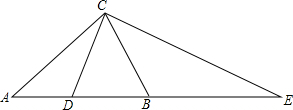 锐角△ABC中,AC=AB,CD是中线,延长AB到E使BE=AB,连接CE,此时△ACE为钝角三角形且∠DCB=36°,则∠DCE的度数是( )
锐角△ABC中,AC=AB,CD是中线,延长AB到E使BE=AB,连接CE,此时△ACE为钝角三角形且∠DCB=36°,则∠DCE的度数是( )| A、60° | B、72° |
| C、66° | D、不确定 |
| 1 |
| 2 |
| A、-1<t<3 | ||
| B、-1≤t<3 | ||
C、
| ||
| D、t≥-1 |
 锐角△ABC中,AC=AB,CD是中线,延长AB到E使BE=AB,连接CE,此时△ACE为钝角三角形且∠DCB=36°,则∠DCE的度数是( )
锐角△ABC中,AC=AB,CD是中线,延长AB到E使BE=AB,连接CE,此时△ACE为钝角三角形且∠DCB=36°,则∠DCE的度数是( )| A、60° | B、72° |
| C、66° | D、不确定 |