题目内容
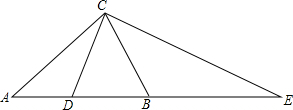 锐角△ABC中,AC=AB,CD是中线,延长AB到E使BE=AB,连接CE,此时△ACE为钝角三角形且∠DCB=36°,则∠DCE的度数是( )
锐角△ABC中,AC=AB,CD是中线,延长AB到E使BE=AB,连接CE,此时△ACE为钝角三角形且∠DCB=36°,则∠DCE的度数是( )| A、60° | B、72° |
| C、66° | D、不确定 |
考点:等腰三角形的性质
专题:
分析:取AC的中点F,连接BF,根据等腰三角形的轴对称性可得∠DCB=∠FBC,再判断出BF是△ACE的中位线,然后根据三角形的中位线平行于第三边并且等于第三边的一半可得BF∥CE,根据两直线平行,内错角相等可得∠BCE=∠FBC,然后根据∠DCE=∠BCE+∠DCB计算即可得解.
解答: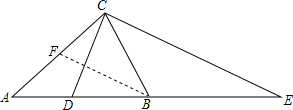 解:如图,取AC的中点F,连接BF,
解:如图,取AC的中点F,连接BF,
∵AC=AB,CD是中线,
∴∠DCB=∠FBC=36°,
∵BE=AB,
∴BF是△ACE的中位线,
∴BF∥CE,
∴∠BCE=∠FBC=36°,
∴∠DCE=∠BCE+∠DCB=36°+36°=72°.
故选B.
 解:如图,取AC的中点F,连接BF,
解:如图,取AC的中点F,连接BF,∵AC=AB,CD是中线,
∴∠DCB=∠FBC=36°,
∵BE=AB,
∴BF是△ACE的中位线,
∴BF∥CE,
∴∠BCE=∠FBC=36°,
∴∠DCE=∠BCE+∠DCB=36°+36°=72°.
故选B.
点评:本题考查了等腰三角形的性质,三角形的中位线平行于第三边并且等于第三边的一半,难点在于作辅助线构造出三角形的中位线.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
 如图,OP是∠AOB的平分线,则下列说法错误的是( )
如图,OP是∠AOB的平分线,则下列说法错误的是( )| A、∠AOB=2∠AOP | ||
B、∠AOP=
| ||
C、∠AOB=
| ||
| D、∠AOP=∠BOP |
 数学课上,探讨角平分线的作法时,小明发现只利用直角三角板也可以作角平分线,操作如下:
数学课上,探讨角平分线的作法时,小明发现只利用直角三角板也可以作角平分线,操作如下: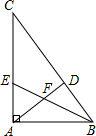 在△ABC中,∠CAB=90°,AD⊥BC于D,BE平分∠CBA交AC于E,交AD于F,求证:AE=AF.
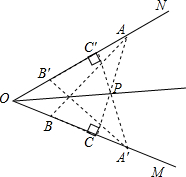
在△ABC中,∠CAB=90°,AD⊥BC于D,BE平分∠CBA交AC于E,交AD于F,求证:AE=AF. 某船在大海上行到O处,沿北偏东60°方向航行2海里后,再沿北偏西30°方向航行2海里,以下面线段AB为一海里,在下图上画同航线.
某船在大海上行到O处,沿北偏东60°方向航行2海里后,再沿北偏西30°方向航行2海里,以下面线段AB为一海里,在下图上画同航线. 已知:如图,二次函数的图象是由y=-x2向右平移1个单位,再向上平移4个单位所得到,这时图象与x轴的交点为A、B(A在B的左边),与y轴交于点C.
已知:如图,二次函数的图象是由y=-x2向右平移1个单位,再向上平移4个单位所得到,这时图象与x轴的交点为A、B(A在B的左边),与y轴交于点C.