题目内容
抛物线y=2x2-5x-3与y轴的交点坐标是 ,与x轴的交点坐标是 .
考点:抛物线与x轴的交点
专题:
分析:要求抛物线与x轴的交点,即令y=0,解方程即可.同理,要求抛物线与y轴的交点,即令x=0,解方程即可.
解答:解:令x=0,则y=-3,即抛物线y=2x2-5x-3与y轴的交点坐标是 (0,-3).
令y=0,则2x2-5x-3=0,即(2x+1)(x-3)=0,
可得:2x+1=0或x-3=0,
解得:x1=-
,x2=3.
则抛物线y=2x2-5x-3与x轴的交点坐标是(-
,0),(3,0).
故答案为(0,-3);(-
,0),(3,0).
令y=0,则2x2-5x-3=0,即(2x+1)(x-3)=0,
可得:2x+1=0或x-3=0,
解得:x1=-
| 1 |
| 2 |
则抛物线y=2x2-5x-3与x轴的交点坐标是(-
| 1 |
| 2 |
故答案为(0,-3);(-
| 1 |
| 2 |
点评:此题考查了抛物线与x轴的交点.求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标,令y=0,即ax2+bx+c=0,解关于x的一元二次方程即可求得交点横坐标.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
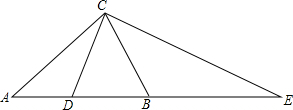 锐角△ABC中,AC=AB,CD是中线,延长AB到E使BE=AB,连接CE,此时△ACE为钝角三角形且∠DCB=36°,则∠DCE的度数是( )
锐角△ABC中,AC=AB,CD是中线,延长AB到E使BE=AB,连接CE,此时△ACE为钝角三角形且∠DCB=36°,则∠DCE的度数是( )| A、60° | B、72° |
| C、66° | D、不确定 |
 如图,△ABC中,AB=AC,BD平分∠ABC交AC于G,DM∥BC交∠ABC的外角平分线于M,交AB,AC于F,E,以下结论:①MB⊥BD,②FD=EC,③EC=EF+DG,④CE=
如图,△ABC中,AB=AC,BD平分∠ABC交AC于G,DM∥BC交∠ABC的外角平分线于M,交AB,AC于F,E,以下结论:①MB⊥BD,②FD=EC,③EC=EF+DG,④CE=| 1 |
| 2 |
| A、1个 | B、2个 | C、3个 | D、4个 |
如图,用同样规格的黑、白两色正方形瓷砖铺设矩形地面,请观察下列图形,探究在第n个图中,黑、白瓷砖分别各有多少块( )


| A、4n+6,n(n+1) |
| B、4n+6,n(n+2) |
| C、n(n+1),4n+6 |
| D、n(n+2),4n+6 |
 如图,∠COD=110°,∠BOD=90°,OA平分∠BOC,求∠AOD的度数.
如图,∠COD=110°,∠BOD=90°,OA平分∠BOC,求∠AOD的度数. 如图,已知抛物线y=
如图,已知抛物线y= 如图,矩形ABCD的边AD长为2,AB长为1,点A在数轴上对应的数是-1,以A点为圆心,对角线AC长为半径画弧,交数轴于点E,则这个点E表示的实数是( )
如图,矩形ABCD的边AD长为2,AB长为1,点A在数轴上对应的数是-1,以A点为圆心,对角线AC长为半径画弧,交数轴于点E,则这个点E表示的实数是( ) 听说中考要考尺规作图,一天,老师在黑板上画了两条线段(如图),要求“以a为底、b为底边上的高,用尺规作一个等腰三角形,并写出已知和求作”.初三的小明早已生疏尺规作图了,请聪明的你帮帮他.
听说中考要考尺规作图,一天,老师在黑板上画了两条线段(如图),要求“以a为底、b为底边上的高,用尺规作一个等腰三角形,并写出已知和求作”.初三的小明早已生疏尺规作图了,请聪明的你帮帮他.