题目内容
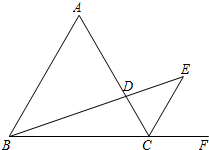 如图,△ABC是等边三角形,CE是外角平分线,点D在AC上,连接BD并延长交CE于点E,若AB=6,AD=2CD,则BE的长为
如图,△ABC是等边三角形,CE是外角平分线,点D在AC上,连接BD并延长交CE于点E,若AB=6,AD=2CD,则BE的长为考点:相似三角形的判定与性质,等边三角形的性质,勾股定理
专题:
分析:如图,作辅助线;证明AB∥CF,得到△ABD∽△CED,进而得到
=
,结合AD=2CD,AB=6,求出CE=3;求出EG、CG的长度,运用勾股定理即可解决问题.
| AB |
| CE |
| AD |
| CD |
解答: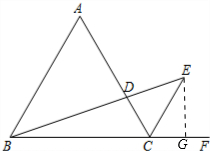 解:如图,过点E作EG⊥CF于点G;
解:如图,过点E作EG⊥CF于点G;
∵△ABC是等边三角形,
∴∠A=∠ACB=60°,AB=BC=6;
∴∠ACF=120°,而CE是外角平分线,
∴∠ACE=∠ECG=60°,∠A=∠ACE,
∴AB∥CF,△ABD∽△CED,
∴
=
,而AD=2CD,AB=6,
∴CE=3;而∠ECG=60°,
∴∠CEG=30°,CG=
CE=1.5,EG=
,
∴BG=7.5;
由勾股定理得:BE2=BG2+EG2,
∴BE=3
,
故答案为3
.
 解:如图,过点E作EG⊥CF于点G;
解:如图,过点E作EG⊥CF于点G;∵△ABC是等边三角形,
∴∠A=∠ACB=60°,AB=BC=6;
∴∠ACF=120°,而CE是外角平分线,
∴∠ACE=∠ECG=60°,∠A=∠ACE,
∴AB∥CF,△ABD∽△CED,
∴
| AB |
| CE |
| AD |
| CD |
∴CE=3;而∠ECG=60°,
∴∠CEG=30°,CG=
| 1 |
| 2 |
3
| ||
| 2 |
∴BG=7.5;
由勾股定理得:BE2=BG2+EG2,
∴BE=3
| 7 |
故答案为3
| 7 |
点评:该题主要考查了等边三角形的性质、相似三角形的判定、勾股定理等几何知识点及其应用问题;解题的关键是作辅助线;灵活运用等边三角形的性质、相似三角形的判定、勾股定理等几何知识点来分析、判断、解答.

练习册系列答案
相关题目
一个长方形的周长是18cm,若这个长方形的长减少1,宽增加2,就可以成为一个正方形,则此正方形的边长是( )
| A、5cm | B、6cm |
| C、7cm | D、8cm |
从点O引两条射线OA、OB,在OA、OB上分别截取OM=1cm,ON=1cm,则M、N两点间的距离一定( )
| A、小于1cm |
| B、大于1cm |
| C、等于1cm |
| D、有最大值2cm |
 小明玩数学游戏,利用四张完全相同的小长方形纸板测量一张正方形纸板的边长,将它们如图放置,测量的数据如图,则这张正方形纸板的边长为( )
小明玩数学游戏,利用四张完全相同的小长方形纸板测量一张正方形纸板的边长,将它们如图放置,测量的数据如图,则这张正方形纸板的边长为( )| A、60cm | B、70cm |
| C、80cm | D、90cm |
 已知:如图,点D、E分别是等边△ABC的两边AB、AC上的点,且AD=CE,求证:CD=BE.
已知:如图,点D、E分别是等边△ABC的两边AB、AC上的点,且AD=CE,求证:CD=BE.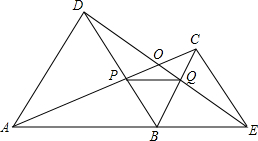 已知△ABD和△BCE均为等边三角形,连接AC,DE交DB于点P,交DE于点O,你能得到哪些结论,并给予证明.
已知△ABD和△BCE均为等边三角形,连接AC,DE交DB于点P,交DE于点O,你能得到哪些结论,并给予证明. 如图,AB是⊙O的直径,点C是⊙O上一点,AD与过点C的切线垂直,垂足为点D,直线DC与AB的延长线相交于点P,弦CE平分∠ACB,交AB于点F,连接BE.
如图,AB是⊙O的直径,点C是⊙O上一点,AD与过点C的切线垂直,垂足为点D,直线DC与AB的延长线相交于点P,弦CE平分∠ACB,交AB于点F,连接BE. 如图所示,点B,C是线段AD上任意两点,点M是AB的中点,点N是CD的中点.若AD=27,BC=5,则线段MN的长是
如图所示,点B,C是线段AD上任意两点,点M是AB的中点,点N是CD的中点.若AD=27,BC=5,则线段MN的长是