题目内容
 已知:如图,点D、E分别是等边△ABC的两边AB、AC上的点,且AD=CE,求证:CD=BE.
已知:如图,点D、E分别是等边△ABC的两边AB、AC上的点,且AD=CE,求证:CD=BE.考点:全等三角形的判定与性质,等边三角形的性质
专题:
分析:根据等边三角形的性质,结合条件可证明△ADC≌△CEB,可得CD=BE.
解答:证明:∵△ABC为等边三角形,
∴AC=BC,∠A=∠ACB=60°,
在△ADC和△CEB中,
,
∴△ADC≌△CEB(SAS),
∴CD=BE.
∴AC=BC,∠A=∠ACB=60°,
在△ADC和△CEB中,
|
∴△ADC≌△CEB(SAS),
∴CD=BE.
点评:本题主要考查全等三角形的判定和性质,掌握全等三角形的判定方法(SSS、SSAS、ASA、AAS和HL)和性质(全等三角形的对应边、对应角相等)是解题的关键.

练习册系列答案
 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案 激活思维优加课堂系列答案
激活思维优加课堂系列答案
相关题目
 如图,在?ABCD中,∠ABD=90°,若AB=3,BC=5,则平行四边形ABCD的面积为
如图,在?ABCD中,∠ABD=90°,若AB=3,BC=5,则平行四边形ABCD的面积为
 如图,线段AB的长为8cm,点C为线段AB任意一点,点M为线段AC的中点,点N为线段BC的中点.
如图,线段AB的长为8cm,点C为线段AB任意一点,点M为线段AC的中点,点N为线段BC的中点. (1)已知线段a,b.用圆规和直尺作线段AC,及线段AC上的点B,使AC=2a+b,其中AB=2a,BC=b.(不写作法但保留作图痕迹);
(1)已知线段a,b.用圆规和直尺作线段AC,及线段AC上的点B,使AC=2a+b,其中AB=2a,BC=b.(不写作法但保留作图痕迹); (1)已知线段AB长为6cm,点C是线段AB上一点,满足AC=
(1)已知线段AB长为6cm,点C是线段AB上一点,满足AC=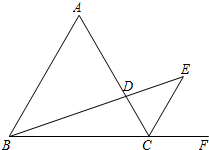 如图,△ABC是等边三角形,CE是外角平分线,点D在AC上,连接BD并延长交CE于点E,若AB=6,AD=2CD,则BE的长为
如图,△ABC是等边三角形,CE是外角平分线,点D在AC上,连接BD并延长交CE于点E,若AB=6,AD=2CD,则BE的长为 如图,B、C两点把线段AD分成2,4,3三部分,点P是AD的中点,已知CD=5,求线段PC的长.
如图,B、C两点把线段AD分成2,4,3三部分,点P是AD的中点,已知CD=5,求线段PC的长.