题目内容
15. 在图中,已知直线AB和直线CD被直线GH所截,交点分别为E,F,∠AEF=∠EFD.
在图中,已知直线AB和直线CD被直线GH所截,交点分别为E,F,∠AEF=∠EFD.(1)直线AB和直线CD平行吗?为什么?
(2)若EM是∠AEF的平分线,FN是∠EFD的平分线,则EM与FN平行吗?为什么?
分析 (1)根据内错角相等,两直线平行,推出即可;
(2)根据角平分线定义求出∠MEF=∠NFE,根据内错角相等,两直线平行,推出即可.
解答 (1)证明:∵∠AEF=∠EFD,
∴AB∥CD(内错角相等,两直线平行).
(2)EM∥FN,
证明:∵ME是∠AEF的平分线,FN是∠EFD的平分线,
∴∠MEF=$\frac{1}{2}$∠AEF,∠NFE=$\frac{1}{2}$∠EFD,
∵∠AEF=∠EFD,
∴∠MEF=∠NFE,
∴EM∥FN(内错角相等,两直线平行).
点评 本题考查了平行线的性质和判定,角平分线的定义等知识点的应用,能熟练地运用性质进行推理是解此题的关键,平行线的判定定理:①同位角相等,两直线平行,②内错角相等,两直线平行,③同旁内角互补,两直线平行.题目比较典型,难度适中.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
6.关于x的分式方程$\frac{2x-a}{x-1}=1$的解为正数,则字母a的取值范围为( )
| A. | a≥1且a≠2 | B. | a>1且a≠2 | C. | a≥1 | D. | a>1 |
3. 如图的矩形ABCD中,E为$\overline{AB}$的中点,有一圆过C、D、E三点,且此圆分别与$\overline{AD}$、$\overline{BC}$相交于P、Q两点.甲、乙两人想找到此圆的圆心O,其作法如下:
如图的矩形ABCD中,E为$\overline{AB}$的中点,有一圆过C、D、E三点,且此圆分别与$\overline{AD}$、$\overline{BC}$相交于P、Q两点.甲、乙两人想找到此圆的圆心O,其作法如下:
(甲) 作∠DEC的角平分线L,作$\overline{DE}$的中垂线,交L于O点,则O即为所求;
(乙) 连接$\overline{PC}$、$\overline{QD}$,两线段交于一点O,则O即为所求
对于甲、乙两人的作法,下列判断何者正确?( )
 如图的矩形ABCD中,E为$\overline{AB}$的中点,有一圆过C、D、E三点,且此圆分别与$\overline{AD}$、$\overline{BC}$相交于P、Q两点.甲、乙两人想找到此圆的圆心O,其作法如下:
如图的矩形ABCD中,E为$\overline{AB}$的中点,有一圆过C、D、E三点,且此圆分别与$\overline{AD}$、$\overline{BC}$相交于P、Q两点.甲、乙两人想找到此圆的圆心O,其作法如下:(甲) 作∠DEC的角平分线L,作$\overline{DE}$的中垂线,交L于O点,则O即为所求;
(乙) 连接$\overline{PC}$、$\overline{QD}$,两线段交于一点O,则O即为所求
对于甲、乙两人的作法,下列判断何者正确?( )
| A. | 两人皆正确 | B. | 两人皆错误 | C. | 甲正确,乙错误 | D. | 甲错误,乙正确 |
7.$\sqrt{16}$的算术平方根是( )
| A. | 2 | B. | 4 | C. | ±2 | D. | ±4 |
4.计算-3x2+4x2的结果为( )
| A. | -7x2 | B. | 7x2 | C. | -x2 | D. | x2 |
5.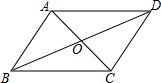 如图,平行四边形ABCD的对角线交于点O,且AB=6,△OCD的周长为19,则?ABCD的两条对角线的和是( )
如图,平行四边形ABCD的对角线交于点O,且AB=6,△OCD的周长为19,则?ABCD的两条对角线的和是( )
 如图,平行四边形ABCD的对角线交于点O,且AB=6,△OCD的周长为19,则?ABCD的两条对角线的和是( )
如图,平行四边形ABCD的对角线交于点O,且AB=6,△OCD的周长为19,则?ABCD的两条对角线的和是( )| A. | 13 | B. | 25 | C. | 26 | D. | 38 |