题目内容
5．
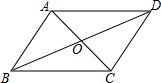如图，平行四边形ABCD的对角线交于点O，且AB=6，△OCD的周长为19，则?ABCD的两条对角线的和是（ ）| A． | 13 | B． | 25 | C． | 26 | D． | 38 |
分析 首先由平行四边形的性质可求出CD的长，由条件△OCD的周长为19，即可求出OD+OC的长，再根据平行四边的对角线互相平分即可求出平行四边形的两条对角线的和．
解答 解：∵四边形ABCD是平行四边形，
∴AB=CD=6，
∵△OCD的周长为19，
∴OD+OC=19-6=13，
∵BD=2DO，AC=2OC，
∴平行四边形ABCD的两条对角线的和=BD+AC=2（DO+OC）=26，
故选：C．
点评 本题主要考查了平行四边形的基本性质，并利用性质解题．熟记平行四边形的性质，由三角形的周长求出OD+OC是解决问题的关键．
练习册系列答案
相关题目
在图中，已知直线AB和直线CD被直线GH所截，交点分别为E，F，∠AEF=∠EFD．
16．如图图形既是轴对称图形又是中心对称图形的是（ ）
| A． |  | B． |  | C． |  | D． |  |
13．若解分式方程$\frac{x-1}{x+4}$=$\frac{m}{x+4}$产生增根，则m=（ ）
| A． | 1 | B． | 0 | C． | -4 | D． | -5 |
20．下列图形中既是轴对称图形又是中心对称图形的是（ ）
| A． |  | B． |  | C． |  | D． |  |
如图，正方形ABCD的边长为2，MN∥BC分别交AB、CD于点M、N，在MN上任取两点P、Q，那么图中阴影部分的面积是2．
15．如果关于x的一元二次方程（a-c）x2-2bx+（a+c）=0有两个相等的实数根，其中a、b、c是△ABC的三边长，那么△ABC的形状是（ ）
| A． | 直角三角形 | B． | 等腰三角形 | C． | 等边三角形 | D． | 等腰直角三角形 |