题目内容
11.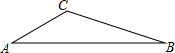 在△ABC中,∠A=30,tanB=$\frac{1}{3}$,BC=$\sqrt{10}$.求AB的长.
在△ABC中,∠A=30,tanB=$\frac{1}{3}$,BC=$\sqrt{10}$.求AB的长.
分析 作CD⊥AB于D,先解Rt△BCD,求出CD、BD;然后在Rt△ACD中利用∠A的正切求出AD的长;那么根据AB=AD+BD即可求解.
解答 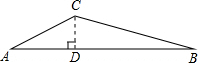 解:作CD⊥AB于D.
解:作CD⊥AB于D.
设CD=x,根据题意得BD=3x.
在Rt△BCD中,由勾股定理得x2+(3x)2=($\sqrt{10}$)2,
解得x=1.
所以CD=1,BD=3.
在Rt△ACD中,∵∠A=30°,tanA=$\frac{CD}{AD}$,
∴AD=$\frac{CD}{tan30°}$=$\sqrt{3}$.
∴AB=AD+BD=$\sqrt{3}$+3.
点评 本题考查了解直角三角形,作辅助线把三角形分解成两个直角三角形,再利用三角函数求解.

练习册系列答案
相关题目
16.一箱啤酒(每箱24瓶)中有4瓶的盖内印有“奖”字,小明的爸爸买了一箱这种品牌的啤酒,但连续打开4瓶均未中奖,此时小明在剩下的啤酒中任意拿一瓶,那么他拿出的这瓶啤酒中奖的机会是( )
| A. | $\frac{1}{24}$ | B. | $\frac{1}{6}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{5}$ |
3.对于函数y=$\frac{6}{x}$,下列说法错误的是( )
| A. | 它的图象分布在第一、三象限 | B. | 当x>0时,y的值随x的增大而增大 | ||
| C. | 它的图象与直线y=-x无交点 | D. | 当x<0时,y的值随x的增大而减小 |
20.下列说法中,正确的是( )
| A. | 负数没有立方根 | B. | 一个数的立方根有两个 | ||
| C. | ($\root{3}{a}$)3=a | D. | $\root{3}{a}$<a |
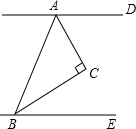 如图,直线AD∥BE,AC、BC分别平分∠BAD、∠ABE,∠CAD=55°,则∠CBE=35°.
如图,直线AD∥BE,AC、BC分别平分∠BAD、∠ABE,∠CAD=55°,则∠CBE=35°.