题目内容
19.设△ABC的垂心为H,BC、AH中点为M、N,以AH为直径的圆交MN于点P,求证:AP平分∠BAC.分析 先作△ABC的外接圆,连接BO并延长交⊙O于点D,连接OA、OM、CD、AD、CH,∴CD⊥BC,AD⊥AB,由点H是△ABC的垂心,易得四边形AHCD是平行四边形,由中位线及外接圆圆心易证四边形AOMN是平行四边形,可得∠OAB=∠CAH,可得出∠OAP+∠OAB=∠PAN+∠CAH,即可求出∠PAB=∠PAC.
解答 证明:如图,作△ABC的外接圆,连接BO并延长交⊙O于点D,连接OA、OM、CD、AD、CH,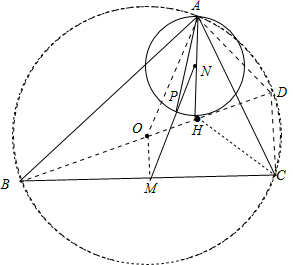
∴CD⊥BC,AD⊥AB,
∵点H是△ABC的垂心
∴AH⊥BC,CH⊥AB
∴AH∥CD,AD∥CH
∴四边形AHCD是平行四边形
∴AH∥CD,AH=CD
∵O是△ABC外接圆圆心,OM⊥BC
∴BM=CM
∴OM是△BCD的中位线
∴OM=$\frac{1}{2}$CD,OM∥CD,
∴OM∥AH,OM=$\frac{1}{2}$AH=AN,
∴四边形AOMN是平行四边形,
∴MN∥OA,
∴∠OAP=∠APN=∠PAN,
∵∠OAB=$\frac{1}{2}$(180°-∠AOB)=90°-∠ACB=∠DCA=∠CAH,
∴∠OAP+∠OAB=∠PAN+∠CAH,即∠PAB=∠PAC,
∴AP平分∠BAC.
点评 本题主要考查了三角形的重心及三角形的外心,解题的关键是正确的作出辅助线,利用圆周角得出∠OAB=∠CAH.

练习册系列答案
相关题目
14.在-5,-9,-3.5,-0.01,-2,-212各数中,最大的数是( )
| A. | -12 | B. | -9 | C. | -0.01 | D. | -5 |
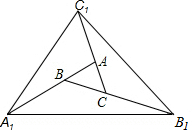 如图,对面积为1的△ABC逐次进行以下操作:第一次操作,分别延长AB、BC、CA至点A1、B1、C1,使得A1B=2AB,B1C=2BC,C1A=2CA,顺次连接A1、B1、C1,得到△A1B1C1,记其面积为S1;第二次操作,分别延长A1B1、B1C1、C1A1至点A2、B2、C2,使得A2B1=2A1B1,B2C1=2B1C1,C2A1=2C1A1,顺次连接A2、B2、C2,得到△A2B2C2,记其面积为S2;按此规律继续下去,可得到△AnBnCn,记其面积为Sn.则S1=19,Sn=19n.
如图,对面积为1的△ABC逐次进行以下操作:第一次操作,分别延长AB、BC、CA至点A1、B1、C1,使得A1B=2AB,B1C=2BC,C1A=2CA,顺次连接A1、B1、C1,得到△A1B1C1,记其面积为S1;第二次操作,分别延长A1B1、B1C1、C1A1至点A2、B2、C2,使得A2B1=2A1B1,B2C1=2B1C1,C2A1=2C1A1,顺次连接A2、B2、C2,得到△A2B2C2,记其面积为S2;按此规律继续下去,可得到△AnBnCn,记其面积为Sn.则S1=19,Sn=19n.
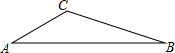 在△ABC中,∠A=30,tanB=$\frac{1}{3}$,BC=$\sqrt{10}$.求AB的长.
在△ABC中,∠A=30,tanB=$\frac{1}{3}$,BC=$\sqrt{10}$.求AB的长.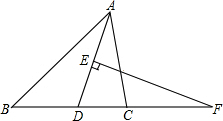 如图,在△ABC中,FD2=FB•FC,AD的垂直平分线交AD于E,交BC的延长线于F,求证:AD平分∠BAC.
如图,在△ABC中,FD2=FB•FC,AD的垂直平分线交AD于E,交BC的延长线于F,求证:AD平分∠BAC.