题目内容
4.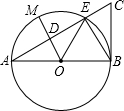 如图,以线段AB为直径的⊙O交线段AC于点E,点M是$\widehat{AE}$的中点,OM交AC于点D,∠BOE=60°,cosC=$\frac{1}{2}$,BC=2$\sqrt{3}$,则MD的长度为( )
如图,以线段AB为直径的⊙O交线段AC于点E,点M是$\widehat{AE}$的中点,OM交AC于点D,∠BOE=60°,cosC=$\frac{1}{2}$,BC=2$\sqrt{3}$,则MD的长度为( )| A. | $\frac{1}{2}$ | B. | $\frac{3}{2}$ | C. | 2 | D. | $\sqrt{3}$ |
分析 如图,要求MD,只要求出OD、OM即可;根据题意容易发现OD为△ABE的中位线,因此应首先求出BE;运用三角函数的定义求出BE;容易证明△OBE为等边三角形,可求出OM=OB=BE,即可解决问题.
解答  解:如图,∵点M是$\widehat{AE}$的中点,
解:如图,∵点M是$\widehat{AE}$的中点,
∴OM⊥AE,AD=DE;而OA=OB,
∴OD是△ABE的中位线,
∴OD=$\frac{1}{2}$BE;
∵OE=OB,且∠BOE=60°,
∴△OBE是等边三角形,
∴OM=OB=BE;
∵AB为⊙O的直径,
∴∠BEC=∠AEB=90°;
∵cosC=$\frac{1}{2}$,
∴$\frac{EC}{BC}=\frac{1}{2}$,而BC=2$\sqrt{3}$,
∴EC=$\sqrt{3}$,BE=3,
∴OD=$\frac{3}{2}$,MD=3-$\frac{3}{2}$=$\frac{3}{2}$,
故选B.
点评 该题主要考查了垂径定理、三角形的中位线定理、锐角三角函数的定义等知识点及其应用问题;解题的关键是牢固掌握垂径定理、三角形的中位线定理等知识点,并能灵活运用、解题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 受台风影响,一棵大树从B处被折断,树的顶部落在离树根底部C相距4米的A处,测得∠CAB=60°,那么这棵树折断前高为14.9米$(结果保留一位小数,\sqrt{3}≈1.73)$.
受台风影响,一棵大树从B处被折断,树的顶部落在离树根底部C相距4米的A处,测得∠CAB=60°,那么这棵树折断前高为14.9米$(结果保留一位小数,\sqrt{3}≈1.73)$.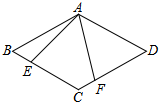 如图,菱形ABCD中,AB=4,∠ABC=60°,∠EAF=60°,∠EAF的两边分别交BC、CD于E、F两点,则CE+CF的值为( )
如图,菱形ABCD中,AB=4,∠ABC=60°,∠EAF=60°,∠EAF的两边分别交BC、CD于E、F两点,则CE+CF的值为( ) 如图,已知△BOC是等腰三角形并且∠A=∠D.求证:AB=DC.
如图,已知△BOC是等腰三角形并且∠A=∠D.求证:AB=DC.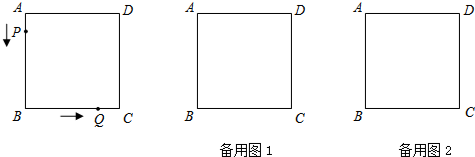
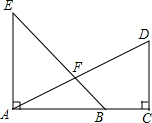 如图,已知AE⊥AC,DC⊥AC,AE=AC,AB=CD,AD与BE互相垂直且相等吗?为什么?
如图,已知AE⊥AC,DC⊥AC,AE=AC,AB=CD,AD与BE互相垂直且相等吗?为什么?