题目内容
3．在?ABCD中，对角线AC，BD相交于点O，AB=8cm，BC=6cm．△AOB的周长是18cm，则△AOD的周长是16cm．分析 先由△AOB的周长求出OA+OB，再由平行四边形的性质得出OA+OD=OA+OB，即可求出△AOD的周长．
解答 解：如图所示：
∵四边形ABCD是平行四边形，
∴OA=OC，OB=OD，AD=BC=6cm，
∵△AOB的周长是18cm，AB=8cm，
∴AB+OA+OB=18cm，
∴OA+OB=10cm，
∴△AOD的周长=OA+OD+AD=OA+OB+AD=10+6=16（cm）；
故答案为：16cm．
点评 本题考查了平行四边形的性质；熟练掌握平行四边形的性质是解决问题的关键．
练习册系列答案
相关题目
如图，将平行四边形ABCD的边DC延长到E，使CE=CD，连接AE交BC于F，∠AFC=n∠D，当n=2时，四边形ABEC是矩形．
8．
如图，A在O的正北方向，B在O的正东方向，且A、B到点O的距离相等．甲从A出发，以每小时60千米的速度朝正东方向行驶，乙从B出发，以每小时40千米的速度朝正北方向行驶，1小时后，位于点O处的观察员发现甲、乙两人之间的夹角为45°，即∠COD=45°，此时甲、乙两人相距（ ）
如图，A在O的正北方向，B在O的正东方向，且A、B到点O的距离相等．甲从A出发，以每小时60千米的速度朝正东方向行驶，乙从B出发，以每小时40千米的速度朝正北方向行驶，1小时后，位于点O处的观察员发现甲、乙两人之间的夹角为45°，即∠COD=45°，此时甲、乙两人相距（ ）| A． | 80千米 | B． | 50$\sqrt{2}$千米 | C． | 100千米 | D． | 100$\sqrt{2}$千米 |
4．
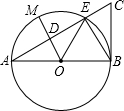如图，以线段AB为直径的⊙O交线段AC于点E，点M是$\widehat{AE}$的中点，OM交AC于点D，∠BOE=60°，cosC=$\frac{1}{2}$，BC=2$\sqrt{3}$，则MD的长度为（ ）
如图，以线段AB为直径的⊙O交线段AC于点E，点M是$\widehat{AE}$的中点，OM交AC于点D，∠BOE=60°，cosC=$\frac{1}{2}$，BC=2$\sqrt{3}$，则MD的长度为（ ）| A． | $\frac{1}{2}$ | B． | $\frac{3}{2}$ | C． | 2 | D． | $\sqrt{3}$ |