题目内容
10．先化简，再求值：$\frac{5a-2b}{{a}^{2}-4{b}^{2}}$•（a-2b），其中a，b满足$\frac{a}{2}$=$\frac{b}{3}$≠0．分析 原式约分得到最简结果，把已知等式变形后代入计算即可求出值．
解答 解：原式=$\frac{5a-2b}{a+2b}$，
由$\frac{a}{2}$=$\frac{b}{3}$，得到a=$\frac{2}{3}$b，
则原式=$\frac{\frac{10}{3}b-2b}{\frac{2}{3}b+2b}$=$\frac{1}{2}$．
点评 此题考查了分式的化简求值，熟练掌握运算法则是解本题的关键．
练习册系列答案
相关题目
20．在面积为15的平行四边形ABCD中，过点A作AE垂直于直线BC于点E，作AF垂直于直线CD于点F，若AB=5，BC=6，则CE+CF的值为（ ）
| A． | 11+$\frac{11\sqrt{3}}{2}$ | B． | 11+$\frac{11\sqrt{3}}{2}$或1+$\frac{\sqrt{3}}{2}$ | ||
| C． | 11+$\frac{11\sqrt{3}}{2}$或11-$\frac{11\sqrt{3}}{2}$ | D． | 11-$\frac{11\sqrt{3}}{2}$ |
1．在$\sqrt{3}$，-1，0，-$\sqrt{2}$这四个数中，最大的是（ ）
| A． | $\sqrt{3}$ | B． | 0 | C． | -1 | D． | -$\sqrt{2}$ |
4．
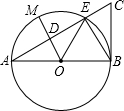如图，以线段AB为直径的⊙O交线段AC于点E，点M是$\widehat{AE}$的中点，OM交AC于点D，∠BOE=60°，cosC=$\frac{1}{2}$，BC=2$\sqrt{3}$，则MD的长度为（ ）
如图，以线段AB为直径的⊙O交线段AC于点E，点M是$\widehat{AE}$的中点，OM交AC于点D，∠BOE=60°，cosC=$\frac{1}{2}$，BC=2$\sqrt{3}$，则MD的长度为（ ）| A． | $\frac{1}{2}$ | B． | $\frac{3}{2}$ | C． | 2 | D． | $\sqrt{3}$ |
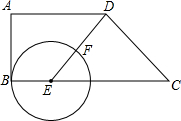在梯形ABCD中，AD∥BC，AB⊥AD，AB=4，AD=5，CD=5．E为底边BC上一点，以点E为圆心，BE为半径画⊙E交射线ED于点F．设BE=y，DF=x．