题目内容
5．
受台风影响，一棵大树从B处被折断，树的顶部落在离树根底部C相距4米的A处，测得∠CAB=60°，那么这棵树折断前高为14.9米$（结果保留一位小数，\sqrt{3}≈1.73）$．
分析 首先利用30°的角所对的直角边是斜边的一半求得AB的长，然后利用勾股定理求得BC的长，从而求得树高即可．
解答 解：∵BC⊥AC，∠BAC=60°，
∴∠B=30°，
∵AC=4，
∴AB=2AC=8米，
∴BC=$\sqrt{{8}^{2}-{4}^{2}}$≈6.9米，
∴树高为AB+BC=8+6.9=14.9米，
故答案为：14.9．
点评 本题考查了勾股定理的应用，解题的关键是从实际问题中抽象出直角三角形并求得斜边的长，难度不大．
练习册系列答案
名校课堂系列答案
相关题目
15．下列调查中，①调查你所在班级同学的年龄情况；②检测杭州的空气质量；③为保证“风云二号08星”成功发射，对其零部件进行检查；④对乘坐某航班的乘客进行安检．其中适合采用抽样调查的是（ ）
| A． | ① | B． | ② | C． | ③ | D． | ④ |
16．一元二次方程x2+4x+4=0的根是（ ）
| A． | x1=4，x2=-4 | B． | x1=x2=-2 | C． | x1=2，x2=-2 | D． | x1=0，x2=-2 |
如图，将平行四边形ABCD的边DC延长到E，使CE=CD，连接AE交BC于F，∠AFC=n∠D，当n=2时，四边形ABEC是矩形．
20．在面积为15的平行四边形ABCD中，过点A作AE垂直于直线BC于点E，作AF垂直于直线CD于点F，若AB=5，BC=6，则CE+CF的值为（ ）
| A． | 11+$\frac{11\sqrt{3}}{2}$ | B． | 11+$\frac{11\sqrt{3}}{2}$或1+$\frac{\sqrt{3}}{2}$ | ||
| C． | 11+$\frac{11\sqrt{3}}{2}$或11-$\frac{11\sqrt{3}}{2}$ | D． | 11-$\frac{11\sqrt{3}}{2}$ |
17．下列说法正确的是（ ）
| A． | $\sqrt{9}$的算术平方根是$\sqrt{3}$ | B． | ±$\frac{3}{4}$是$\frac{9}{16}$的算术平方根 | ||
| C． | -8的立方根是2 | D． | 0没有平方根 |
4．
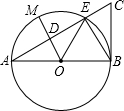如图，以线段AB为直径的⊙O交线段AC于点E，点M是$\widehat{AE}$的中点，OM交AC于点D，∠BOE=60°，cosC=$\frac{1}{2}$，BC=2$\sqrt{3}$，则MD的长度为（ ）
如图，以线段AB为直径的⊙O交线段AC于点E，点M是$\widehat{AE}$的中点，OM交AC于点D，∠BOE=60°，cosC=$\frac{1}{2}$，BC=2$\sqrt{3}$，则MD的长度为（ ）| A． | $\frac{1}{2}$ | B． | $\frac{3}{2}$ | C． | 2 | D． | $\sqrt{3}$ |