题目内容
9．
如图，已知△BOC是等腰三角形并且∠A=∠D．求证：AB=DC．
分析 由AAS证明△AOB≌△DOC，根据全等三角形的对应边相等即可得出结论．
解答 证明：∵△BOC是等腰三角形，
∴OB=OC，
在△AOB和△DOC中，$\left\{\begin{array}{l}{∠A=∠D}\\{∠AOB=∠DOC}\\{OB=OC}\end{array}\right.$，
∴△AOB≌△DOC（AAS），
∴AB=DC．
点评 本题考查了全等三角形的判定与性质；证明三角形全等是解决问题的关键．
练习册系列答案
相关题目
8．
如图，A在O的正北方向，B在O的正东方向，且A、B到点O的距离相等．甲从A出发，以每小时60千米的速度朝正东方向行驶，乙从B出发，以每小时40千米的速度朝正北方向行驶，1小时后，位于点O处的观察员发现甲、乙两人之间的夹角为45°，即∠COD=45°，此时甲、乙两人相距（ ）
如图，A在O的正北方向，B在O的正东方向，且A、B到点O的距离相等．甲从A出发，以每小时60千米的速度朝正东方向行驶，乙从B出发，以每小时40千米的速度朝正北方向行驶，1小时后，位于点O处的观察员发现甲、乙两人之间的夹角为45°，即∠COD=45°，此时甲、乙两人相距（ ）| A． | 80千米 | B． | 50$\sqrt{2}$千米 | C． | 100千米 | D． | 100$\sqrt{2}$千米 |
4．
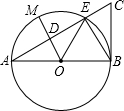如图，以线段AB为直径的⊙O交线段AC于点E，点M是$\widehat{AE}$的中点，OM交AC于点D，∠BOE=60°，cosC=$\frac{1}{2}$，BC=2$\sqrt{3}$，则MD的长度为（ ）
如图，以线段AB为直径的⊙O交线段AC于点E，点M是$\widehat{AE}$的中点，OM交AC于点D，∠BOE=60°，cosC=$\frac{1}{2}$，BC=2$\sqrt{3}$，则MD的长度为（ ）| A． | $\frac{1}{2}$ | B． | $\frac{3}{2}$ | C． | 2 | D． | $\sqrt{3}$ |
18．数轴上A，B，C三点所表示的数分别为a，b，c，且点C在线段AB上，若|a|=|b|，且线段AC的长度是线段CB的3倍，则下列有关a，b，c的式子，表示正确的是（ ）
| A． | |c|=$\frac{1}{2}$|b| | B． | |c|=$\frac{1}{3}$|b| | C． | |c|=$\frac{1}{4}$|b| | D． | |c|=$\frac{3}{4}$|b| |