题目内容
 如图是一个三角点阵,从上向下数有无数多行,其中第一行有1个点,第二行有2个点…,第n行有n个点…,若该三角点阵前n行的点数和为300,则n的值为( )
如图是一个三角点阵,从上向下数有无数多行,其中第一行有1个点,第二行有2个点…,第n行有n个点…,若该三角点阵前n行的点数和为300,则n的值为( )| A、30 | B、26 | C、25 | D、24 |
考点:规律型:图形的变化类
专题:
分析:由于第一行有1个点,第二行有2个点…第n行有n个点…,则前五行共有(1+2+3+4+5)个点,前10行共有(1+2+3+4+5+6+7+8+9+10)个点,前n行共有1+2+3+4+5+…+n=
n(n+1)个点,然后建立方程求出n的数值即可.
| 1 |
| 2 |
解答:解:由题意得:
n(n+1)=300
解得:n=24.
故选:D.
| 1 |
| 2 |
解得:n=24.
故选:D.
点评:本题考查了图形的变化规律,通过从一些特殊的数字变化中发现不变的因素或按规律变化的因素,然后推广到一般情况.

练习册系列答案
 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
在平面直角坐标系中,将抛物线y=x2+1向右平移2个单位,再向下平移4个单位,得到的抛物线的解析式是( )
| A、y=(x+2)2-3 |
| B、y=(x-2)2-3 |
| C、y=(x-2)2+5 |
| D、y=(x+2)2+5 |
 从正面、上面、左面三个方向看某一个物体得到的图形如图所示,则这个物体是( )
从正面、上面、左面三个方向看某一个物体得到的图形如图所示,则这个物体是( )| A、圆锥 | B、圆柱 |
| C、三棱锥 | D、三棱柱 |
 如图,当一个点从O出发,沿15°线移动1个单位长度(即OP长为1个单位长度),这个点在竖直方向上升了约0.26个单位长度,在水平方向前进了约0.97个单位长度,sin15°约等于( )
如图,当一个点从O出发,沿15°线移动1个单位长度(即OP长为1个单位长度),这个点在竖直方向上升了约0.26个单位长度,在水平方向前进了约0.97个单位长度,sin15°约等于( )| A、3.73 | B、0.97 |
| C、0.50 | D、0.26 |
 写出图中所有同位角、内错角、同旁内角.
写出图中所有同位角、内错角、同旁内角.
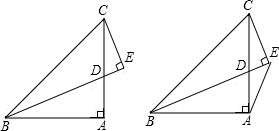 如图,已知在△ABC中,∠BAC为直角,AB=AC,CE⊥BD于E.
如图,已知在△ABC中,∠BAC为直角,AB=AC,CE⊥BD于E.