题目内容
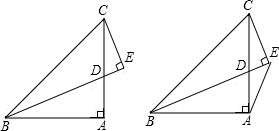 如图,已知在△ABC中,∠BAC为直角,AB=AC,CE⊥BD于E.
如图,已知在△ABC中,∠BAC为直角,AB=AC,CE⊥BD于E.(1)若BE平分∠CBE,求证:BD=2EC;
(2)若D为AC上一动点(不与C,A重合),则∠AED的大小是否变化?若变化,求出变化范围;若不变,求出大小.
考点:全等三角形的判定与性质
专题:
分析:(1)由于DB是∠CBA的平分线,且BE⊥CE,可根据等腰三角形三线合一的特点来作辅助线;延长CE交BA的延长线于F,可先证△BEC≌△BEF,得出CE=EF=
CF;然后证△BDA≌△CFA,得出BD=CF;由此可得证.
(2)∠AED的度数应该不变;如果过A分别作BD、CF的垂线,设垂足为H、G,则四边形AHEG是矩形;由(1)的全等三角形知:AH=AG(全等三角形对应的高线相等),故四边形AHEG是正方形,而AE正好是正方形的对角线,故∠AED=45°.
| 1 |
| 2 |
(2)∠AED的度数应该不变;如果过A分别作BD、CF的垂线,设垂足为H、G,则四边形AHEG是矩形;由(1)的全等三角形知:AH=AG(全等三角形对应的高线相等),故四边形AHEG是正方形,而AE正好是正方形的对角线,故∠AED=45°.
解答: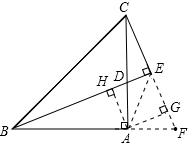 解(1)延长BA、CE相交于点F,
解(1)延长BA、CE相交于点F,
∵BE平分∠CBE,BE⊥CE,
∴BC=BF,
在△BEC与△BEF中,
,
∴△BEC≌△BEF(HL),
∴CE=FE,
∴CE=
CF,
∵∠BAC是直角,
∴∠BAD=∠CAF=90°,
∵∠F+∠FBE=∠FCA+∠F=90°,
∴∠ACF=∠FBE,
即∠ACF=∠ABD,
又∵AC=AB,
在△BAD与△CAF中,
,
∴△BAD≌△CAF(ASA),
∴BD=CF,即CE=
BD.
(2)∠AEB不变为45°.
理由如下:
过点A作AH⊥BE垂足为H,作AG⊥CE交CE延长线于G,
由(1)知∠ACF=∠ABD,
在△BAH与△CAG中,
,
∴△BAH≌△CAG(AAS)
∴AH=AG,
∵AH⊥EB,AG⊥EG,
∴EA平分∠BEF,
∴∠BEA=
∠BEG=45°.
 解(1)延长BA、CE相交于点F,
解(1)延长BA、CE相交于点F,∵BE平分∠CBE,BE⊥CE,
∴BC=BF,
在△BEC与△BEF中,
|
∴△BEC≌△BEF(HL),
∴CE=FE,
∴CE=
| 1 |
| 2 |
∵∠BAC是直角,
∴∠BAD=∠CAF=90°,
∵∠F+∠FBE=∠FCA+∠F=90°,
∴∠ACF=∠FBE,
即∠ACF=∠ABD,
又∵AC=AB,
在△BAD与△CAF中,
|
∴△BAD≌△CAF(ASA),
∴BD=CF,即CE=
| 1 |
| 2 |
(2)∠AEB不变为45°.
理由如下:
过点A作AH⊥BE垂足为H,作AG⊥CE交CE延长线于G,
由(1)知∠ACF=∠ABD,
在△BAH与△CAG中,
|
∴△BAH≌△CAG(AAS)
∴AH=AG,
∵AH⊥EB,AG⊥EG,
∴EA平分∠BEF,
∴∠BEA=
| 1 |
| 2 |
点评:本题考查的是全等三角形的判定和性质,正确的构建出与所求和已知相关的全等三角形,是解答本题的关键.

练习册系列答案
相关题目
下列函数中,y随x的增大而增大的是( )
| A、y=-2x+3 | ||
B、y=-
| ||
C、y=
| ||
| D、y=-2x2(x>0) |
 如图,直线AB、CD相交于点O,则∠AOD的度数是( )
如图,直线AB、CD相交于点O,则∠AOD的度数是( )| A、120° | B、100° |
| C、75° | D、150° |
 如图,DE∥BC,则下列比例式错误的是( )
如图,DE∥BC,则下列比例式错误的是( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 原图画有三角形ABC及其经过平移所得的三角形A′B′C′,但其中过顶点C和B′的4条边都被擦去了(如图).
原图画有三角形ABC及其经过平移所得的三角形A′B′C′,但其中过顶点C和B′的4条边都被擦去了(如图). 如图是一个三角点阵,从上向下数有无数多行,其中第一行有1个点,第二行有2个点…,第n行有n个点…,若该三角点阵前n行的点数和为300,则n的值为( )
如图是一个三角点阵,从上向下数有无数多行,其中第一行有1个点,第二行有2个点…,第n行有n个点…,若该三角点阵前n行的点数和为300,则n的值为( ) 已知关于m的方程
已知关于m的方程 如图,点O是△ABC内任意一点,且△ABC为等边三角形,高为3cm,则O到三边的距离之和为?
如图,点O是△ABC内任意一点,且△ABC为等边三角形,高为3cm,则O到三边的距离之和为?