题目内容
3．a为有理数，a3+a2+a+1=0，1+a+a2+a3+…+a2016=1．分析 首先将1+a+a2+a3+…+a2016变形为：1+a（a+a2+a3）+a5（1+a+a2+a3）…+a2013（1+a+a2+a3），然后将a3+a2+a+1=0代入即可求得答案．
解答 解：∵a3+a2+a+1=0，
∴1+a+a2+a3+…+a2016
=1+a（1+a+a2+a3）+a5（1+a+a2+a3）…+a2013（1+a+a2+a3）
=1．
故答案为：1．
点评 此题考查了因式分解的应用，分组分解与整体代入是求得答案的关键．
练习册系列答案
相关题目
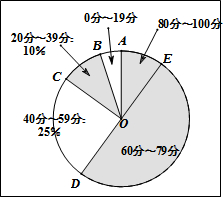如图是某学校的一次健康知识测验的分数段统计图（满分100分，分数均为整数），点O是圆心，点D，O，E在同一条直线上，∠AOE=36°．