题目内容
13.小敏在文具店买了三种贴纸:普通贴纸每张8角,荧光贴纸每张1元,高级贴纸每张2元.她一共用了12.2元.那么小敏买的三种贴纸的总数量最少是多少张?分析 设普通贴纸x张,荧光贴纸y张,高级贴纸z张,价格分别为0.8元,1元,2元,所以能够保证总数尾数为0.2元的只能是0.8元,因为0.8×4=32,0.8×9=72;另价格最高的越多,贴纸就越少,依此分析即可求解.
解答 解:8角=0.8元,
设普通贴纸x张,荧光贴纸y张,高级贴纸z张,根据题意可得方程:
0.8x+y+2z=12.2,
因为能够保证总数尾数为0.2元的只能是0.8元,因为0.8×4=3.2,0.8×9=7.2;另价格最高的越多,8角就越少,
所以当x=4时,y+2z=9,所以z最大为4,则y=1,
4+1+4=9(张).
答:小敏买的三种贴纸的总数量最少是9张.
点评 此题考查了利用不定方程的整数解解决实际问题的灵活应用,此题关键是根据12.2元的末位数字得出8角信的封数,抓住价格最高的越多,贴纸的总数量就越少,即可得出8角的贴纸的张数.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
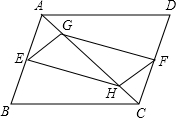 如图,四边形ABCD为平行四边形,BE=DF,AG=CH.求证:四边形EHFG为平行四边形.
如图,四边形ABCD为平行四边形,BE=DF,AG=CH.求证:四边形EHFG为平行四边形.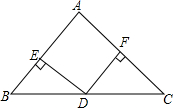 在△ABC中,AB=AC,D是BC的中点,DE⊥AB,DF⊥AC,垂足分别是E,F
在△ABC中,AB=AC,D是BC的中点,DE⊥AB,DF⊥AC,垂足分别是E,F