题目内容
2.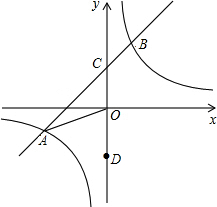 如图,在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象与反比例函数y=$\frac{m}{x}$(m≠0)的图象交于一、三象限内的A、B两点,与y轴交于C点,点B的坐标为(3,n).线段AO=13,D为y轴上一点,且sin∠AOD=$\frac{5}{13}$.
如图,在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象与反比例函数y=$\frac{m}{x}$(m≠0)的图象交于一、三象限内的A、B两点,与y轴交于C点,点B的坐标为(3,n).线段AO=13,D为y轴上一点,且sin∠AOD=$\frac{5}{13}$.(1)求该反比例函数和一次函数的解析式;
(2)求△AOC的面积;
(3)求不等式kx+b-$\frac{m}{x}$<0的解集(直接写出答案)
分析 (1)过点A作AD⊥x轴于D点,由sin∠AOD=$\frac{5}{13}$,OA=13,根据正弦的定义可求出AD,再根据勾股定理得到DO,即得到A点坐标(-5,-12),把A(-5,-12)代入y=$\frac{m}{x}$,确定反比例函数的解析式为y=$\frac{60}{x}$;将B(3,n)代入,确定点B点坐标,然后把A点和B点坐标代入y=ax+b,求出a和b,即可得到结论;
(2)先令x=0,求出C点坐标,得到OC的长,然后根据三角形的面积公式计算△AOC的面积即可;
(3)根据函数的图象和交点坐标即可求得.
解答 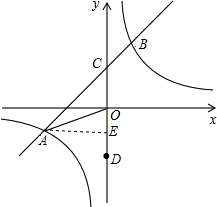 解:(1)过点A作AE⊥x轴于E点,如图,
解:(1)过点A作AE⊥x轴于E点,如图,
∵sin∠AOD=$\frac{5}{13}$,OA=13,
∴sin∠AOE=$\frac{AE}{OA}$=$\frac{AE}{13}$=$\frac{5}{13}$,
∴AE=5,
∴EO=$\sqrt{1{3}^{2}-{5}^{2}}$=12,
而点A在第三象限,
∴点A的坐标为(-5,-12),
将A(-5,-12)代入y=$\frac{m}{x}$,得m=60,
∴反比例函数的解析式为y=$\frac{60}{x}$;
将B(3,n)代入y=$\frac{60}{x}$,得n=20;
将A(-5,-12)和B(3,20)分别代入y=ax+b,得
$\left\{\begin{array}{l}{-5a+b=-12}\\{3a+b=20}\end{array}\right.$解得:$\left\{\begin{array}{l}{a=4}\\{b=8}\end{array}\right.$,
∴所求的一次函数的解析式为y=4x+8;
(2)在y=4x+8中,令x=0,
即y=8
∴C点坐标为(0,8),即OC=8,
∴S△AOC=$\frac{1}{2}$•AE•OC=$\frac{1}{2}×5×8$=20;
(3)不等式kx+b-$\frac{m}{x}$<0的解集为:x<-5,或0<x<3.
点评 此题考查了反比例函数与一次函数的交点问题.其知识点有解直角三角形,待定系数法求解析,解方程组等,此题难度适中,注意掌握数形结合思想与方程思想的应用.

 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案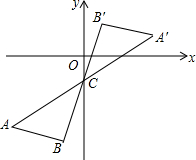 如图,将△ABC绕点C(0,-2)旋转180°得到△A′B′C′,设点A的坐标为(m,n)则点A′的坐标为( )
如图,将△ABC绕点C(0,-2)旋转180°得到△A′B′C′,设点A的坐标为(m,n)则点A′的坐标为( )| A. | (-m,-n) | B. | (-m,-n-2) | C. | (-m,-n+2) | D. | (-m,-n-4) |
| A. | y=-x | B. | y=-x+6 | C. | y=-x+3 | D. | y=-$\frac{\sqrt{3}}{3}$x+6 |
 如图,△ABC的两条高AD、BE相交于点G,且AD=BD.
如图,△ABC的两条高AD、BE相交于点G,且AD=BD.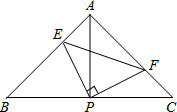 如图,已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE、PF分别交AB、AC于点E、F,给出以下四个结论:
如图,已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE、PF分别交AB、AC于点E、F,给出以下四个结论: 如图,四边形ABCD中,AB=DC,∠A=∠D,M、N分别是AD、BC的中点,E、F分别是BM、CM的中点,求证:四边形MENF是菱形.
如图,四边形ABCD中,AB=DC,∠A=∠D,M、N分别是AD、BC的中点,E、F分别是BM、CM的中点,求证:四边形MENF是菱形. 已知:实数a,b在数轴上的位置如图所示,化简:$\sqrt{(a+1)^{2}}$+2$\sqrt{(b-1)^{2}}$-|a-b|.
已知:实数a,b在数轴上的位置如图所示,化简:$\sqrt{(a+1)^{2}}$+2$\sqrt{(b-1)^{2}}$-|a-b|.