题目内容
12.在直角坐标系中,一直线a向下平移3个单位后所得直线b经过点A(0,3),将直线b绕点A顺时针旋转75°后所得直线经过点B(-$\sqrt{3}$,0),则直线a的函数关系式为( )| A. | y=-x | B. | y=-x+6 | C. | y=-x+3 | D. | y=-$\frac{\sqrt{3}}{3}$x+6 |
分析 根据题意画出图象,进而利用旋转的性质得出C点坐标,进而得出其解析式,再求出平移前的解式即可.
解答  解:如图所示:由题意可得:∠BAC=75°,
解:如图所示:由题意可得:∠BAC=75°,
∵A(0,3),B(-$\sqrt{3}$,0),
∴BO=$\sqrt{3}$,AO=3,
∴tan∠BAO=$\frac{\sqrt{3}}{3}$,
则∠BAO=30°,
∴∠OAC=45°,
则AO=CO=3,故C(3,0),
∴设直线b的解析式为:y=kx+3,
则0=3k+3,
解得:k=-1,
则直线b的解析式为:y=-x+3,
∵一直线a向下平移3个单位后所得直线b,
∴直线a的函数关系式为:y=-x+6.
故选:B.
点评 本题考查了一次函数图象与几何变换,解决本题的关键是得到直线b的解析式.

练习册系列答案
相关题目
1.下列图形中,形如中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
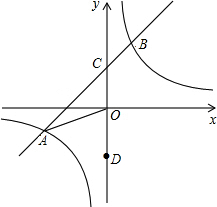 如图,在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象与反比例函数y=$\frac{m}{x}$(m≠0)的图象交于一、三象限内的A、B两点,与y轴交于C点,点B的坐标为(3,n).线段AO=13,D为y轴上一点,且sin∠AOD=$\frac{5}{13}$.
如图,在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象与反比例函数y=$\frac{m}{x}$(m≠0)的图象交于一、三象限内的A、B两点,与y轴交于C点,点B的坐标为(3,n).线段AO=13,D为y轴上一点,且sin∠AOD=$\frac{5}{13}$. 已知:如图,点E在△ABC的边BA延长线上,AD∥BC,∠B=∠C.求证:AD平分∠EAC.
已知:如图,点E在△ABC的边BA延长线上,AD∥BC,∠B=∠C.求证:AD平分∠EAC.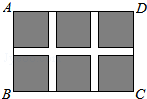 如图,某小区规划在一个长30m、宽20m的长方形ABCD上修建三条同样宽的通道,使其中两条与AB平行,另一条与AD平行,其余部分种花草.要使每一块花草的面积都为78m2,那么通道的宽应设计成多少m?
如图,某小区规划在一个长30m、宽20m的长方形ABCD上修建三条同样宽的通道,使其中两条与AB平行,另一条与AD平行,其余部分种花草.要使每一块花草的面积都为78m2,那么通道的宽应设计成多少m?