题目内容
3.画出y=2x与y=x+2的图象,它们有交点吗?交点坐标是什么?解方程组$\left\{\begin{array}{l}{y=2x}\\{y=x+2}\end{array}\right.$,比较交点坐标与方程组的解,从中你发现了什么?分析 利用描点法画出两函数图象得到它们的交点坐标,再利用代入法解方程组,然后比较交点坐标与方程组的解,可得到方程组的解就是两个相应的一次函数图象的交点坐标.
解答 解:如图,y=2x与y=x+2的图象,它们有交点,交点坐标位(2,4);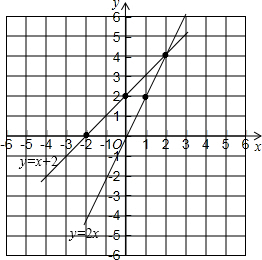
$\left\{\begin{array}{l}{y=2x①}\\{y=x+2②}\end{array}\right.$,
把①代入②得2x=x+2,解得x=2,
把x=2代入①得y=4,
所以方程组的解为$\left\{\begin{array}{l}{x=2}\\{y=4}\end{array}\right.$,
比较交点坐标与方程组的解,得到方程组的解就是两个相应的一次函数图象的交点坐标.
点评 本题考查了一次函数与二元一次方程组:方程组的解就是使方程组中两个方程同时成立的一对未知数的值,而这一对未知数的值也同时满足两个相应的一次函数式,因此方程组的解就是两个相应的一次函数图象的交点坐标.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
14.如果一个多边形的外角分别是10°,20°,30°…,那么这个多边形是( )
| A. | 六边形 | B. | 七边形 | C. | 八边形 | D. | 九边形 |
19.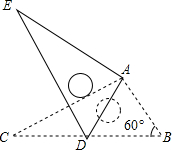 如图,将Rt△ABC绕点A按顺时针旋转一定角度得到Rt△ADE,点B的对应点D恰好落在BC边上,若AB=1,∠B=60°,则△ABD的面积为( )
如图,将Rt△ABC绕点A按顺时针旋转一定角度得到Rt△ADE,点B的对应点D恰好落在BC边上,若AB=1,∠B=60°,则△ABD的面积为( )
 如图,将Rt△ABC绕点A按顺时针旋转一定角度得到Rt△ADE,点B的对应点D恰好落在BC边上,若AB=1,∠B=60°,则△ABD的面积为( )
如图,将Rt△ABC绕点A按顺时针旋转一定角度得到Rt△ADE,点B的对应点D恰好落在BC边上,若AB=1,∠B=60°,则△ABD的面积为( )| A. | 2$\sqrt{3}$ | B. | $\sqrt{3}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{3}}{4}$ |
 (1)设二次函数y=ax2+bx+c(a≠0)图象如图所示,经过点(-1,0),试判断a、b、c、a+b+c、a-b+c、b2-4ac的符号
(1)设二次函数y=ax2+bx+c(a≠0)图象如图所示,经过点(-1,0),试判断a、b、c、a+b+c、a-b+c、b2-4ac的符号 如图是一个物体的三视图,根据图中尺寸(单位:cm),它的体积为32+8πcm3.
如图是一个物体的三视图,根据图中尺寸(单位:cm),它的体积为32+8πcm3.