题目内容
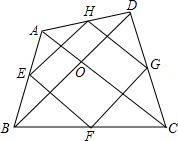 如图,在四边形ABCD中,AC=BD,对角线AC,BD交于点0,AC丄BD,E,F,G,H分别AB,BC,CD,DA的中点.
如图,在四边形ABCD中,AC=BD,对角线AC,BD交于点0,AC丄BD,E,F,G,H分别AB,BC,CD,DA的中点.求证:四边形EFGH是正方形.
考点:中点四边形
专题:证明题
分析:先由三角形的中位线定理求出四边相等,然后由AC⊥BD入手,进行正方形的判断.
解答:证明:在△ABC中,E、F分别是AB、BC的中点,
故可得:EF=
AC,同理FG=
BD,GH=
AC,HE=
BD,
在四边形ABCD中,AC=BD,
∴EF=FG=GH=HE,
∴四边形EFGH是菱形.
在△ABD中,E、H分别是AB、AD的中点,
则EH∥BD,
同理GH∥AC,
又∵AC⊥BD,
∴EH⊥HG,
∴四边形EFGH是正方形.
故可得:EF=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
在四边形ABCD中,AC=BD,
∴EF=FG=GH=HE,
∴四边形EFGH是菱形.
在△ABD中,E、H分别是AB、AD的中点,
则EH∥BD,
同理GH∥AC,
又∵AC⊥BD,
∴EH⊥HG,
∴四边形EFGH是正方形.
点评:此题考查了正方形的判定,解题的关键是了解既是矩形又是菱形的四边形是正方形,难度适中.

练习册系列答案
相关题目
 如图,在?ABCD中,E为BC上一点,且AD=DE,AE、DC的延长线交于点F,∠ADE=50°,求∠CEF的度数.
如图,在?ABCD中,E为BC上一点,且AD=DE,AE、DC的延长线交于点F,∠ADE=50°,求∠CEF的度数. 如图所示,四边形ABCD是正方形,延长BC到点F,使CF=AC,连接AF交CD于点E,求∠AEC的度数.
如图所示,四边形ABCD是正方形,延长BC到点F,使CF=AC,连接AF交CD于点E,求∠AEC的度数. 如图,在菱形ABCD中,∠A=60°,AB=4,O是对角线BD的中点,过O点作OE丄AB,垂足为E.
如图,在菱形ABCD中,∠A=60°,AB=4,O是对角线BD的中点,过O点作OE丄AB,垂足为E. 如图所示,已知∠1=65°,∠2=115°,∠3=115°,请用两种不同方法说明AB∥CD.
如图所示,已知∠1=65°,∠2=115°,∠3=115°,请用两种不同方法说明AB∥CD.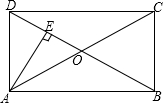 如图所示,已知矩形ABCD的对角线AC与BD相交于点0,AE丄BD于点E,且DE=OE,则∠OAB=
如图所示,已知矩形ABCD的对角线AC与BD相交于点0,AE丄BD于点E,且DE=OE,则∠OAB=