题目内容
 如图,在?ABCD中,E为BC上一点,且AD=DE,AE、DC的延长线交于点F,∠ADE=50°,求∠CEF的度数.
如图,在?ABCD中,E为BC上一点,且AD=DE,AE、DC的延长线交于点F,∠ADE=50°,求∠CEF的度数.考点:平行四边形的性质
专题:几何图形问题
分析:首先根据等边对等角可得∠DAE=∠DEA,再根据三角形内角和定理计算出∠DAE=∠AED=65°,根据平行线的性质可得∠DAE=∠BEA=65°,再根据对顶角相等可得答案.
解答:解:∵AD=DE,
∴∠DAE=∠DEA,
∵∠ADE=50°,
∴∠DAE=∠AED=65°,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠DAE=∠BEA=65°,
∴∠CEF=65°.
∴∠DAE=∠DEA,
∵∠ADE=50°,
∴∠DAE=∠AED=65°,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠DAE=∠BEA=65°,
∴∠CEF=65°.
点评:此题主要考查了平行四边形的性质,以及三角形内角和定理,关键是掌握平行四边形对边平行.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
 如图,在平面直角坐标系中,梯形ABCD的坐标为A(0,0),B(0,8),C(8,8),D(12,0),点P,Q分别从B,D出发以1个单位/秒和2个单位/秒的速度向C,O运动,设运动时间为t(s)(-点到达,另一点也停止运动).
如图,在平面直角坐标系中,梯形ABCD的坐标为A(0,0),B(0,8),C(8,8),D(12,0),点P,Q分别从B,D出发以1个单位/秒和2个单位/秒的速度向C,O运动,设运动时间为t(s)(-点到达,另一点也停止运动). 如图,在△ABC中,∠BAC=45°,AD⊥BC于D点,已知BD=6,CD=4,求高AD的长.
如图,在△ABC中,∠BAC=45°,AD⊥BC于D点,已知BD=6,CD=4,求高AD的长.
 小云参加跳远比赛,他从地面跳板P处起跳落到沙坑中,两脚印分别为A,B两点,人未站稳,一只手撑到沙坑C点,如图所示.请你画出小云跳远成绩所在的垂线段,并说明理由?
小云参加跳远比赛,他从地面跳板P处起跳落到沙坑中,两脚印分别为A,B两点,人未站稳,一只手撑到沙坑C点,如图所示.请你画出小云跳远成绩所在的垂线段,并说明理由?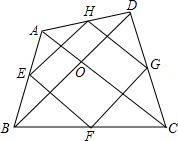 如图,在四边形ABCD中,AC=BD,对角线AC,BD交于点0,AC丄BD,E,F,G,H分别AB,BC,CD,DA的中点.
如图,在四边形ABCD中,AC=BD,对角线AC,BD交于点0,AC丄BD,E,F,G,H分别AB,BC,CD,DA的中点.