题目内容
 如图所示,四边形ABCD是正方形,延长BC到点F,使CF=AC,连接AF交CD于点E,求∠AEC的度数.
如图所示,四边形ABCD是正方形,延长BC到点F,使CF=AC,连接AF交CD于点E,求∠AEC的度数.考点:正方形的性质,等腰三角形的性质
专题:几何图形问题
分析:根据正方形的性质得出∠ACB=45°,再由CF=AC,求出∠F=22.5°,根据三角形的外角性质得出∠AEC=∠F+∠DCF,代入求出即可.
解答:解:∵四边形ABCD是正方形,
∴∠BCD=∠D=90°,
∴∠ACB=
∠DCB=
×90°=45°,∠DCF=90°,
∵AC=CF,
∴∠F=∠CAF,
∵∠F+∠CAF=∠ACB=45°,
∴∠F=
×45°=22.5°,
∴∠AEC=∠F+∠DCF=22.5°+90°=112.5°.
答:∠AEC的度数是112.5°.
∴∠BCD=∠D=90°,
∴∠ACB=
| 1 |
| 2 |
| 1 |
| 2 |
∵AC=CF,
∴∠F=∠CAF,
∵∠F+∠CAF=∠ACB=45°,
∴∠F=
| 1 |
| 2 |
∴∠AEC=∠F+∠DCF=22.5°+90°=112.5°.
答:∠AEC的度数是112.5°.
点评:本题考查了正方形性质,三角形的外角性质的应用,主要考查学生灵活运用正方形性质进行推理和计算的能力.

练习册系列答案
相关题目
 小云参加跳远比赛,他从地面跳板P处起跳落到沙坑中,两脚印分别为A,B两点,人未站稳,一只手撑到沙坑C点,如图所示.请你画出小云跳远成绩所在的垂线段,并说明理由?
小云参加跳远比赛,他从地面跳板P处起跳落到沙坑中,两脚印分别为A,B两点,人未站稳,一只手撑到沙坑C点,如图所示.请你画出小云跳远成绩所在的垂线段,并说明理由? 如图,点P是矩形ABCD外一点,且PA=PB.
如图,点P是矩形ABCD外一点,且PA=PB. 如图所示,CE是BC的延长线.
如图所示,CE是BC的延长线. 为了了解我市某学校“书香校园”的建设情况,检查组在该校随机抽取40名学生,调查了解他们一周阅读课外书籍的財间,并将调査结果绘制成如图所示的频数分布直方图(每小组的时间包含最小值,不包含最大值).
为了了解我市某学校“书香校园”的建设情况,检查组在该校随机抽取40名学生,调查了解他们一周阅读课外书籍的財间,并将调査结果绘制成如图所示的频数分布直方图(每小组的时间包含最小值,不包含最大值).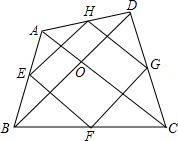 如图,在四边形ABCD中,AC=BD,对角线AC,BD交于点0,AC丄BD,E,F,G,H分别AB,BC,CD,DA的中点.
如图,在四边形ABCD中,AC=BD,对角线AC,BD交于点0,AC丄BD,E,F,G,H分别AB,BC,CD,DA的中点.