题目内容
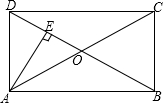如图所示，已知矩形ABCD的对角线AC与BD相交于点0，AE丄BD于点E，且DE=OE，则∠OAB=考点：矩形的性质
专题：几何图形问题
分析：根据矩形的性质得出OA=OD=OB，根据线段垂直平分线性质求出AD=AO，得出等边三角形ADO，求出∠ADO即可．
解答：解：∵四边形ABCD是矩形，
∴∠DAB=90°，AC=BD，AO=OC，BO=DO，
∴OD=OA=OB，
∵AE丄BD，DE=OE，
∴AD=AO，
∴△AOD是等边三角形，
∴∠ADO=60°，
∵∠DAB=90°，OA=OB，
∴∠OAB=∠OBA=30°，
故答案为：30°．
∴∠DAB=90°，AC=BD，AO=OC，BO=DO，
∴OD=OA=OB，
∵AE丄BD，DE=OE，
∴AD=AO，
∴△AOD是等边三角形，
∴∠ADO=60°，
∵∠DAB=90°，OA=OB，
∴∠OAB=∠OBA=30°，
故答案为：30°．
点评：本题考查了矩形性质，线段垂直平分线，等腰三角形性质的应用，解此题的关键是求出∠ADB=60°．
练习册系列答案
一线名师权威作业本系列答案
相关题目
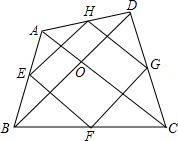如图，在四边形ABCD中，AC=BD，对角线AC，BD交于点0，AC丄BD，E，F，G，H分别AB，BC，CD，DA的中点．
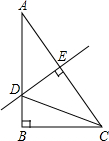如图，在Rt△ABC中，∠A=30°，DE垂直平分斜边AC，交于D，E为垂足，连接CD，若BD=1，求AC的长．
如图，直线AB∥CD，若△ACO的面积为3cm2，则△BDO的面积为
如图，在平行四边形ABCD中，AB=5，AD=8，∠BAD、∠ADC的平分线分别交BC于E、F两点，则EF=