题目内容
9.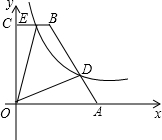 如图,在直角梯形OABC中,BC∥AO,∠AOC=90°,点A,B的坐标分别为(5,0),(2,6),点D为AB上一点,且BD=2AD,函数y=$\frac{k}{x}$(k>0)经过点D,交BC于点E.
如图,在直角梯形OABC中,BC∥AO,∠AOC=90°,点A,B的坐标分别为(5,0),(2,6),点D为AB上一点,且BD=2AD,函数y=$\frac{k}{x}$(k>0)经过点D,交BC于点E.(1)求k的值;
(2)求四边形ODBE的面积.
分析 (1)作BH⊥OA于H,DF⊥OA于F,如图,易得BH=6,BC=2,OA=5,AH=3,证明△ADF∽△ABH,利用相似比可计算出DF=2,AF=1,则可确定D(4,2),然后根据反比例函数图象上点的坐标特征得k=8;
(2)利用反比例函数的几何意义得到S△COE=4,根据三角形面积公式和梯形面积公式得到S△OAD=5,S梯形OABC=21,然后利用S四边形ODBE=S梯形OABC-S△CDE-S△OAD进行计算.
解答 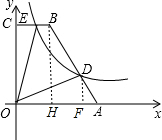 解:(1)作BH⊥OA于H,DF⊥OA于F,如图,
解:(1)作BH⊥OA于H,DF⊥OA于F,如图,
∵点A,B的坐标分别为(5,0),(2,6),
∴BH=6,BC=2,OA=5,
∴AH=5-2=3,
∵DF∥BH,
∴△ADF∽△ABH,
∴$\frac{DF}{BH}$=$\frac{AF}{AH}$=$\frac{AD}{AB}$,即$\frac{DF}{6}$=$\frac{AF}{3}$=$\frac{1}{3}$,
∴DF=2,AF=1,
∴OF=OA-AF=4,
∴D(4,2),
∴k=4×2=8;
(2)∵S△COE=$\frac{1}{2}$×8=4,S△OAD=$\frac{1}{2}$×5×2=5,S梯形OABC=$\frac{1}{2}$×(2+5)×6=21,
∴S四边形ODBE=S梯形OABC-S△CDE-S△OAD=21-4-5=12.
点评 本题考查了反比例函数与一次函数的交点问题:求反比例函数与一次函数的交点坐标,把两个函数关系式联立成方程组求解,若方程组有解则两者有交点,方程组无解,则两者无交点.也考查了反比例函数图象上点的坐标特征和相似三角形的判定与性质.

练习册系列答案
相关题目
14.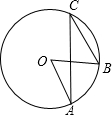 如图,在⊙O中,点A、B、C是圆上的点,连接OA、OB、AC、BC,若∠CAO=20°,∠CBO=50°,∠AOB的度数是( )
如图,在⊙O中,点A、B、C是圆上的点,连接OA、OB、AC、BC,若∠CAO=20°,∠CBO=50°,∠AOB的度数是( )
 如图,在⊙O中,点A、B、C是圆上的点,连接OA、OB、AC、BC,若∠CAO=20°,∠CBO=50°,∠AOB的度数是( )
如图,在⊙O中,点A、B、C是圆上的点,连接OA、OB、AC、BC,若∠CAO=20°,∠CBO=50°,∠AOB的度数是( )| A. | 30° | B. | 40° | C. | 50° | D. | 60° |
18.不等式组$\left\{\begin{array}{l}{x+1>0}\\{x-1≥0}\end{array}\right.$的解集是( )
| A. | 1<x≤1 | B. | -1<x≤1 | C. | x≥1 | D. | x>-1 |
19.将二次函数y=x2-1的图象向右平移一个单位长度,再向上平移3个单位长度所得的抛物线的解析式为( )
| A. | y=(x-1)2+2 | B. | y=(x+1)2+2 | C. | y=(x-1)2-2 | D. | y=(x+1)2-2 |
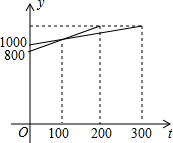 一次越野跑中,当小明跑了1000米时,小刚跑了800米,小明、小刚在此后所跑的路程y(米)与时间t(秒)之间的函数关系如图所示,则这次越野跑的全程为1600米.
一次越野跑中,当小明跑了1000米时,小刚跑了800米,小明、小刚在此后所跑的路程y(米)与时间t(秒)之间的函数关系如图所示,则这次越野跑的全程为1600米.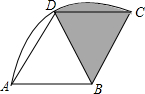 如图,菱形ABCD的边长为2,∠ADC=120°,弧CD是以点B为圆心BC长为半径的弧.则图中阴影部分的面积为$\frac{2π}{3}$(结果保留π).
如图,菱形ABCD的边长为2,∠ADC=120°,弧CD是以点B为圆心BC长为半径的弧.则图中阴影部分的面积为$\frac{2π}{3}$(结果保留π).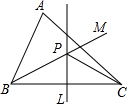 如图,锐角三角形ABC中,直线PL为BC的垂直平分线,射线BM为∠ABC的平分线,PL与BM相交于P点.若∠PBC=30°,∠ACP=20°,则∠A的度数为70°.
如图,锐角三角形ABC中,直线PL为BC的垂直平分线,射线BM为∠ABC的平分线,PL与BM相交于P点.若∠PBC=30°,∠ACP=20°,则∠A的度数为70°.