题目内容
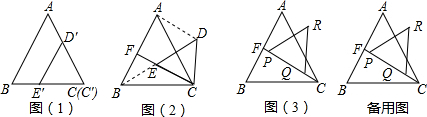
19.如图(1),是边长分别为4$\sqrt{3}$cm和4cm的两个等边三角形纸片ABC和C′D′E′叠放在一起(点C与C′重合)(1)操作:固定△ABC,将△C′D′E′绕点C顺时针旋转30°得到△CDE,连接AD、BE、CE的延长线交AB于点F,如图(2).
探究:在图(2)中,线段BE与AD之间有怎样的大小关系?试证明你的结论;
(2)操作:将图(2)中的△CDE,在射线CF上沿着CF方向平移,平移后的△CDE设为△PQR,如图(3).
探究:设CQ的长度为xcm(0<x<6),△PQR与△ABC重叠部分的面积为ycm2,请直接写出y与x之间的函数关系式,不需要写出求解过程.
分析 (1)BE=AD.证明△BCD≌△ACD,即可得出结论;
(2)画出图形,分三种情况:0<x≤2,2<x≤4,4<x<6分类讨论即可.
解答 解:(1)BE=AD .
.
证明:如答图1,∵△ABC与△DCE都是等边三角形,
∴∠ACB=∠DCE=60°,CA=CB,CE=CD,
∴∠BCE=∠ACD,
在△BCD和△ACD中
$\left\{\begin{array}{l}{CA=CB}\\{∠BCE=∠ACD}\\{CE=CD}\end{array}\right.$,
∴△BCD≌△ACD,
∴BE=AD.
(2)∵∠BCF=30°,∠B=60°
∴∠BFC=90°,
∵△ABC的边长是4$\sqrt{3}$cm,
∴CF=6cm,
∵△PQR的边长是4cm,
∴S△PQR=4$\sqrt{3}$,
设CQ的长度为xcm(0<x<6),
如答图2,当0<x≤2时,QE=CQ=x,
∴ER=4-x,
∵PR⊥AC,∠R=60°,
∴DR=$\frac{1}{2}$(4-x),DE=$\frac{\sqrt{3}}{2}$(4-x),
∴S△DER=$\frac{1}{2}$×$\frac{1}{2}$(4-x)×$\frac{\sqrt{3}}{2}$(4-x)=$\frac{\sqrt{3}}{8}$(4-x)2,
∴S=S△PQR-S△DER=4$\sqrt{3}$-$\frac{\sqrt{3}}{8}$(4-x)2=-$\frac{\sqrt{3}}{8}{x}^{2}+\sqrt{3}x+2\sqrt{3}$;
如答图3,当2<x≤4时,QE=CQ=x,
∴DR=$\frac{1}{2}$(4-x),DE=$\frac{\sqrt{3}}{2}$(4-x),PF=x-2,PG=$\sqrt{3}$(x-2),
∴S△DER=$\frac{1}{2}$×$\frac{1}{2}$(4-x)×$\frac{\sqrt{3}}{2}$(4-x)=$\frac{\sqrt{3}}{8}$(4-x)2,
S△PFG=$\frac{1}{2}$×(x-2)×$\sqrt{3}$(x-2)=$\frac{\sqrt{3}}{2}$(x-2)2,
∴S=S△PQR-S△DER-S△PFG=4$\sqrt{3}$-$\frac{\sqrt{3}}{8}$(4-x)2-$\frac{\sqrt{3}}{2}$(x-2)2=-$\frac{5\sqrt{3}}{8}{x}^{2}+3\sqrt{3}x$;
如答图4,当4<x<6时,QE=CQ=x,
∴FQ=6-x,FM=$\sqrt{3}$(6-x),
∴S△FQM=$\frac{1}{2}$×(6-x)×$\sqrt{3}$(6-x)=$\frac{\sqrt{3}}{2}$(6-x)2,
∴S=S△PQR-S△FQM=4$\sqrt{3}$-$\frac{\sqrt{3}}{2}$(6-x)2=$\frac{\sqrt{3}}{2}{x}^{2}-6\sqrt{3}x+18\sqrt{3}$;
综上所述,S=$\left\{\begin{array}{l}{-\frac{\sqrt{3}}{8}{x}^{2}+\sqrt{3}x+2\sqrt{3}(0<x≤2)}\\{-\frac{5\sqrt{3}}{8}{x}^{2}+3\sqrt{3}x(2<x≤4)}\\{\frac{\sqrt{3}}{2}{x}^{2}-6\sqrt{3}x+18\sqrt{3}(4<x<6)}\end{array}\right.$.
点评 本题主要考查了等边三角形的性质、全等三角形的判定与性质、勾股定理、三角形面积的表示以及列函数表达式的综合应用,第2小题能够画出图形,分类讨论是解决问题的关键.

 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案| A. | $\frac{a}{a+2}$ | B. | $\frac{1}{a}$ | C. | $\frac{1}{a+2}$ | D. | $\frac{1}{a-2}$ |
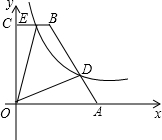 如图,在直角梯形OABC中,BC∥AO,∠AOC=90°,点A,B的坐标分别为(5,0),(2,6),点D为AB上一点,且BD=2AD,函数y=$\frac{k}{x}$(k>0)经过点D,交BC于点E.
如图,在直角梯形OABC中,BC∥AO,∠AOC=90°,点A,B的坐标分别为(5,0),(2,6),点D为AB上一点,且BD=2AD,函数y=$\frac{k}{x}$(k>0)经过点D,交BC于点E.