题目内容
13.若x+y=10,xy=1,则x3y+xy3的值是98.分析 可将该多项式分解为xy(x2+y2),又因为x2+y2=(x+y)2-2xy,然后将x+y与xy的值代入即可.
解答 解:x3y+xy3
=xy(x2+y2)
=xy[(x+y)2-2xy]
=1×(102-2×1)
=98.
故答案为:98.
点评 本题考查了因式分解和代数式变形.解决本类问题的一般方法:若已知x+y与xy的值,则x2+y2=(x+y)2-2xy,再将x+y与xy的值代入即可.

练习册系列答案
相关题目
4.计算|-8|-(-$\frac{1}{2}$)0的值是( )
| A. | -7 | B. | 7 | C. | 7$\frac{1}{2}$ | D. | 9 |
1. 如图是3个相同的小正方体组合而成的几何体,它的俯视图是( )
如图是3个相同的小正方体组合而成的几何体,它的俯视图是( )
 如图是3个相同的小正方体组合而成的几何体,它的俯视图是( )
如图是3个相同的小正方体组合而成的几何体,它的俯视图是( )| A. |  | B. |  | C. |  | D. |  |
8.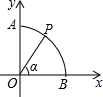 如图,以圆O为圆心,半径为1的弧交坐标轴于A,B两点,P是$\widehat{AB}$上一点(不与A,B重合),连接OP,设∠POB=α,则点P的坐标是( )
如图,以圆O为圆心,半径为1的弧交坐标轴于A,B两点,P是$\widehat{AB}$上一点(不与A,B重合),连接OP,设∠POB=α,则点P的坐标是( )
 如图,以圆O为圆心,半径为1的弧交坐标轴于A,B两点,P是$\widehat{AB}$上一点(不与A,B重合),连接OP,设∠POB=α,则点P的坐标是( )
如图,以圆O为圆心,半径为1的弧交坐标轴于A,B两点,P是$\widehat{AB}$上一点(不与A,B重合),连接OP,设∠POB=α,则点P的坐标是( )| A. | (sinα,sinα) | B. | (cosα,cosα) | C. | (cosα,sinα) | D. | (sinα,cosα) |
5. 如图是加工零件的尺寸要求,现有下列直径尺寸的产品(单位:mm),其中不合格的是( )
如图是加工零件的尺寸要求,现有下列直径尺寸的产品(单位:mm),其中不合格的是( )
 如图是加工零件的尺寸要求,现有下列直径尺寸的产品(单位:mm),其中不合格的是( )
如图是加工零件的尺寸要求,现有下列直径尺寸的产品(单位:mm),其中不合格的是( )| A. | Φ45.02 | B. | Φ44.9 | C. | Φ44.98 | D. | Φ45.01 |
2.下列计算正确的是( )
| A. | a3+a3=a6 | B. | 3a-a=3 | C. | (a3)2=a5 | D. | a•a2=a3 |
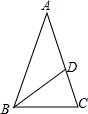 如图,在△ABC中,AB=AC=1,BC=$\frac{\sqrt{5}-1}{2}$,在AC边上截取AD=BC,连接BD.
如图,在△ABC中,AB=AC=1,BC=$\frac{\sqrt{5}-1}{2}$,在AC边上截取AD=BC,连接BD.