题目内容
15.如图所示,AB∥CD.(1)如图1,求证:∠E=∠B+∠D;
(2)如图2,∠B、∠D、∠E有什么关系,直接写出结论,不用证明.
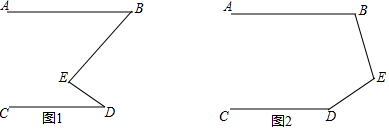
分析 (1)过点E作EF∥AB,由AB∥CD,可得AB∥EF∥CD,再由平行线的性质即可得出结论;
(2)过点E作EF∥AB,由AB∥CD,可得AB∥EF∥CD,根据两直线平行,同旁内角互补,即可求得∠B+∠BED+∠D=360°;
解答 解:(1)如图1,过点E作EF∥AB,
∵AB∥EF,
∴∠B=∠BEF.
∵AB∥CD,
∴EF∥CD,
∴∠D=∠DEF,
∴∠DEB=∠BEF+∠DEF=∠B+∠D;
(2)∠B+∠D+∠E=360°.理由如下:
如图2,过点E作EF∥AB,
又∵AB∥CD,
∴AB∥EF∥CD,
∴∠B+∠BEF=180°,∠FED+∠D=180°,
∴∠B+∠BED+∠D=360°.
点评 此题考查了平行线的性质,根据题意作出平行线,利用平行线的性质求解是解答此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
10.在一个不透明的布袋中,红色、黑色、白色的玻璃球共有40个,除颜色外其他完全相同,小明通过多次摸球试验后发现其中摸到红色球、黑色球的频率分别稳定在0.15和0.45,则口袋中白色球的个数可能是( )
| A. | 28 | B. | 24 | C. | 16 | D. | 6 |
7.某农机厂四月份生产零件50万个,第二季度共生产临建182万个.设该厂五、六月份平均每月的增长率为x,那么x满足的方程是( )
| A. | 50+50(1+x)+50(1+x)2=182 | B. | 50(1+x)2=182 | ||
| C. | 50(1+2x)=182 | D. | 50+50(1+x)+50(1+2x)=182 |
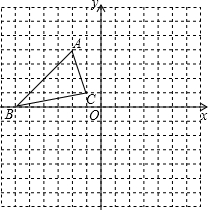 如图,已知△ABC的三个顶点的坐标分别为A(-2,4)、B(-6,0)、C(-1,1).
如图,已知△ABC的三个顶点的坐标分别为A(-2,4)、B(-6,0)、C(-1,1).
 已知:如图,线段m,n,l.
已知:如图,线段m,n,l.