题目内容
3.计算:(1)3xy•(2x3y)2+(-2x3y)3÷2x2
(2)(2x+3)(3-2x)+(2x-1)2
(3)先化简,再求值:[(xy+1)(xy-1)+2(xy+1)2-1]÷xy,其中x=-2,y=$\frac{1}{2}$.
分析 (1)原式利用幂的乘方与积的乘方运算法则计算,合并即可得到结果;
(2)原式利用平方差公式及完全平方公式化简,去括号合并即可得到结果;
(3)原式中括号中利用平方差公式,完全平方公式化简,去括号合并后利用多项式除以单项式法则计算得到最简结果,把x与y的值代入计算即可求出值.
解答 解:(1)原式=3xy•4x6y2-8x9y3÷2x2=12x7y3-4x7y3=8x7y3;
(2)原式=9-4x2+4x2-4x+1=-4x+10;
(3)原式=(x2y2-1+2x2y2+4xy+2-1)÷xy=3xy+4,
当x=-2,y=$\frac{1}{2}$时,原式=-3+4=1.
点评 此题考查了整式的混合运算-化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
13.一根头发丝的半径约为0.00003米,0.00003用科学记数法表示为( )
| A. | 3×10-4 | B. | 3×10-5 | C. | 3×10-6 | D. | 0.3×10-4 |
11.某市政部门计划对一段长为6000m的道路进行整修改造,为尽可能减少施工对交通所造成的影响,在施工过程中增加机械和人力,每天比原计划多修250m,结果提前4天完成任务,设原计划每天施工xm,那么根据题意,可列方程为( )
| A. | $\frac{6000}{x}$-$\frac{6000}{x-250}$=4 | B. | $\frac{6000}{x-250}$-$\frac{6000}{x}$=4 | ||
| C. | $\frac{6000}{x}$-$\frac{6000}{x+250}$=4 | D. | $\frac{6000}{x+250}$-$\frac{6000}{x}$=4 |
18. 如图,下列条件中,能够判断BE∥AC的是( )
如图,下列条件中,能够判断BE∥AC的是( )
 如图,下列条件中,能够判断BE∥AC的是( )
如图,下列条件中,能够判断BE∥AC的是( )| A. | ∠C=∠ABE | B. | ∠C=∠ABC | C. | ∠A=∠ABC | D. | ∠A=∠ABE |
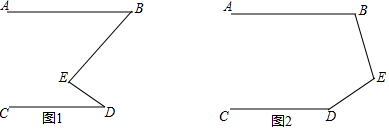
 为了解某新品种黄瓜的生长情况,抽查了部分黄瓜株上长出的黄瓜根数,得到下面的条形图,观察该图,可知共抽查了60株黄瓜,并可估计出这个新品种黄瓜平均每株结出的黄瓜根数是( )
为了解某新品种黄瓜的生长情况,抽查了部分黄瓜株上长出的黄瓜根数,得到下面的条形图,观察该图,可知共抽查了60株黄瓜,并可估计出这个新品种黄瓜平均每株结出的黄瓜根数是( ) 如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF,下列结论:①△ABG≌△AFG;②BG=CG;③AG∥CF;④S△EFC=$\frac{12}{5}$.其中正确结论的是①②③④(只填序号).
如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF,下列结论:①△ABG≌△AFG;②BG=CG;③AG∥CF;④S△EFC=$\frac{12}{5}$.其中正确结论的是①②③④(只填序号).