题目内容
5. 已知:如图,已知点A、B、C在⊙O上,且点B是$\widehat{AC}$的中点,当OA=5cm,cos∠OAB=$\frac{3}{5}$时.
已知:如图,已知点A、B、C在⊙O上,且点B是$\widehat{AC}$的中点,当OA=5cm,cos∠OAB=$\frac{3}{5}$时.(1)求△OAB的面积;
(2)联结AC,求弦AC的长.
分析 (1)过O作OH⊥AB于H,根据cos∠OAB=$\frac{3}{5}$,得到$\frac{AH}{AO}=\frac{3}{5}$,求得AH=3cm,OH=4cm,AB=2AH=6cm,根据三角形的面积公式即可进行求解;
(2)设AC交OB于M,由B是$\widehat{AC}$的中点,得到$\widehat{AB}=\widehat{BC}$,求出AB=BC,推出OB垂直平分AC,即可得到结论.
解答 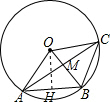 解:(1)过O作OH⊥AB于H,
解:(1)过O作OH⊥AB于H,
∵cos∠OAB=$\frac{3}{5}$,
∴$\frac{AH}{AO}=\frac{3}{5}$,
∴AH=3cm,OH=4cm,AB=2AH=6cm,
∴S△OAB=$\frac{1}{2}$AB•OH=12cm2;
(2)设AC交OB于M,∵B是$\widehat{AC}$的中点,
∴$\widehat{AB}=\widehat{BC}$,∴AB=BC,
∵OA=OC,
故O,B均在线段AC的垂直平分线上,
∴OB垂直平分AC,
∴AM=AB•sin∠MBA=6×$\frac{4}{5}$=$\frac{24}{5}$,
∴AC=2AM=$\frac{48}{5}$cm.
点评 本题考查了垂径定理,解直角三角形,线段垂直平分线的判定和性质,正确的作出辅助线构造直角三角形是解题的关键.

练习册系列答案
相关题目
 如图:用8块相同的长方形拼成一个宽为48厘米的大长方形,每块小长方形的长和宽分别是多少?
如图:用8块相同的长方形拼成一个宽为48厘米的大长方形,每块小长方形的长和宽分别是多少? 如图,以G(0,1)为圆心,半径为2的圆与x轴交于A、B两点,与y轴交于C、D两点,点E为⊙G上一动点,CF⊥AE于F,当点E从B点出发顺时针运动到D点时,点F经过的路径长为$\frac{\sqrt{3}}{3}$π.
如图,以G(0,1)为圆心,半径为2的圆与x轴交于A、B两点,与y轴交于C、D两点,点E为⊙G上一动点,CF⊥AE于F,当点E从B点出发顺时针运动到D点时,点F经过的路径长为$\frac{\sqrt{3}}{3}$π. 如图,△ABC中,AB=AC,AB=4,BD=3,CD∥AB,BD⊥AC于E,求DE的长.
如图,△ABC中,AB=AC,AB=4,BD=3,CD∥AB,BD⊥AC于E,求DE的长. 如图,已知△ABC是等边三角形,D是BC的中点,BH∥AC.
如图,已知△ABC是等边三角形,D是BC的中点,BH∥AC.