题目内容
14. 如图,已知△ABC是等边三角形,D是BC的中点,BH∥AC.
如图,已知△ABC是等边三角形,D是BC的中点,BH∥AC.(1)作图:过D作BH的垂线,分别交AC,BH于E,F,交AB的延长线G;
(2)在图中找出一对全等三角形,并证明你的结论.
分析 (1)过点D作DF⊥BH于F,交AC于E,交直线AB于G;
(2)利用“ASA”可证明△DEC≌△DFB.
解答 解:(1)作图,EG为所作;
(2)△DEC≌△DFB.
证明如下:
∵BH∥AC
∴∠DCE=∠DBF,
又∵D是BC中点,
∴DC=DB,
在△DEC与△DFB中,
$\left\{\begin{array}{l}{∠DCE=∠DBF}\\{DC=DB}\\{∠EDC=∠FDB}\end{array}\right.$,
∴△DEC≌△DFB(ASA).
点评 本题考查了作图-复杂作图:复杂作图是在五种基本作图的基础上进行作图,一般是结合了几何图形的性质和基本作图方法.解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.也考查了全等三角形的判定.

练习册系列答案
相关题目
4.(-1)4可表示为( )
| A. | (-1)×4 | B. | (-1)+(-1)+(-1)+(-1) | C. | -1×1×1×1 | D. | (-1)×(-1)×(-1)×(-1) |
 在锐角三角形ABC中,AB=6,AD是BC边上的高,BD=3,AC=3$\sqrt{6}$,求∠C的度数.
在锐角三角形ABC中,AB=6,AD是BC边上的高,BD=3,AC=3$\sqrt{6}$,求∠C的度数. 已知:如图,已知点A、B、C在⊙O上,且点B是$\widehat{AC}$的中点,当OA=5cm,cos∠OAB=$\frac{3}{5}$时.
已知:如图,已知点A、B、C在⊙O上,且点B是$\widehat{AC}$的中点,当OA=5cm,cos∠OAB=$\frac{3}{5}$时.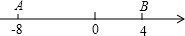 如图,数轴上两个动点A、B起始位置所表示的数分别为-8,4,A、B两点各自以一定的速度在数轴上运动,已知A点的运动速度为2个单位/秒.
如图,数轴上两个动点A、B起始位置所表示的数分别为-8,4,A、B两点各自以一定的速度在数轴上运动,已知A点的运动速度为2个单位/秒. 探究:如图,已知直线l1,l2,l3相互平行,在直线l1上任意一点A作为直角顶点,求作等腰直角三角形△ABC,使点B、C分别落在直线l2和l3上.请你给出作图方法并说明你的作图方法正确的理由.
探究:如图,已知直线l1,l2,l3相互平行,在直线l1上任意一点A作为直角顶点,求作等腰直角三角形△ABC,使点B、C分别落在直线l2和l3上.请你给出作图方法并说明你的作图方法正确的理由. 如图,在等边△ABC中,O为BC边上一点,E为AC边上一点,且∠ADE=6O°,BD=3,CE=2,则AB的长为9.
如图,在等边△ABC中,O为BC边上一点,E为AC边上一点,且∠ADE=6O°,BD=3,CE=2,则AB的长为9. 已知,建立如图所示的直角坐标系,正方形网格中的△ABC,若小方格边长为1,请你根据所学的知识:
已知,建立如图所示的直角坐标系,正方形网格中的△ABC,若小方格边长为1,请你根据所学的知识: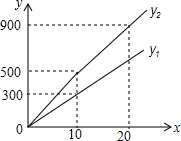 为发展旅游经济,我市某景区对门票采用灵活的售票方法吸引游客.门票定价为50元/人,非节假日打a折售票,节假日按团队人数分段定价售票,即m人以下(含m人)的团队按原价售票;超过m人的团队,其中m人仍按原价售票,超过m人部分的游客打b折售票.设某旅游团人数为x人,非节假日购票款为y1(元),节假日购票款为y2(元).y1与y2之间的函数图象如图所示.
为发展旅游经济,我市某景区对门票采用灵活的售票方法吸引游客.门票定价为50元/人,非节假日打a折售票,节假日按团队人数分段定价售票,即m人以下(含m人)的团队按原价售票;超过m人的团队,其中m人仍按原价售票,超过m人部分的游客打b折售票.设某旅游团人数为x人,非节假日购票款为y1(元),节假日购票款为y2(元).y1与y2之间的函数图象如图所示.