题目内容
18.阅读:探究线段的和.差.倍.分关系是几何中常见的问题,解决此类问题通常会用截长法或补短法,具体做法是在某条线段上截取一条线段与特定线段相等,或是将某条线段延长,使之与特定线段相等,再利用三角形全等的有关性质加以说明.(1)请完成下题的证明过程:如图1,在△ABC中,∠B=2∠C,AD平分∠BAC.求证:AB+BD=AC.证明:在AC上截取AE=AB,连接DE
(2)如图2,AD∥BC,EA,EB分别平分∠DAB,∠CBA,CD过点E,求证:AB=AD+BC.
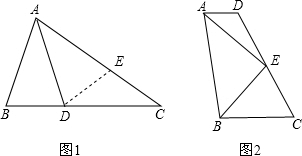
分析 (1)在AC上截取AE=AB,连接DE,证明△ABD≌△AED,得到∠B=∠AED,再证明ED=EC即可;
(2)先过E作EF∥AD,交AB于F,则∠DAE=∠AEF,∠EBC=∠BEF,因为EA、EB分别平分∠DAB和∠CBA,所以AF=EF=FB,再根据梯形中位线定理得出AB=AD+BC.
解答 证明:在AC上截取AE=AB,连接DE,如图1:
∵AD平分∠BAC,
∴∠BAD=∠DAC,
在△ABD和△AED中,
$\left\{\begin{array}{l}{AE=AB}\\{∠BAD=∠DAC}\\{AD=AD}\end{array}\right.$,
∴△ABD≌△AED(SAS),
∴∠B=∠AED,BD=DE,又∠B=2∠C,
∴∠AED=2∠C,
而∠AED=∠C+∠EDC=2∠C,
∴∠C=∠EDC,
∴DE=CE,
∴AB+BD=AE+CE=AC;
(2)过E作EF∥AD,交AB于F,如图2:
则∠DAE=∠AEF,∠EBC=∠BEF,
∵EA、EB分别平分∠DAB和∠CBA,
∴∠EAF=∠AEF,∠EBF=∠BEF,
∴AF=EF=FB,
又∵EF∥AD∥BC,
∴EF是梯形ABCD的中位线,
∴EF=$\frac{AD+BC}{2}$,
∴AF+FB=2EF,
∴AB=AD+BC.
点评 本题考查了全等三角形的判定和性质;此题利用了全等三角形中常用辅助线-截长补短法构造全等三角形,然后利用全等三角形解题,这是解决线段和差问题最常用的方法,注意掌握.

练习册系列答案
相关题目
7.用配方法解方程2x2+3x-1=0,则方程可变形为( )
| A. | (x+3)2=$\frac{1}{3}$ | B. | (x+$\frac{3}{4}$)2=$\frac{1}{2}$ | C. | (3x+1)2=1 | D. | (x+$\frac{3}{4}$)2=$\frac{17}{16}$ |
 如图,在△ABC中,BD、CE是高,G、F分别是BC、DE的中点,连接GF,求证:GF⊥DE.
如图,在△ABC中,BD、CE是高,G、F分别是BC、DE的中点,连接GF,求证:GF⊥DE.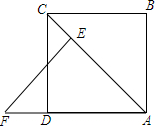 如图,AC是正方形ABCD的对角线,△ABC经过旋转后到达△AEF的位置
如图,AC是正方形ABCD的对角线,△ABC经过旋转后到达△AEF的位置 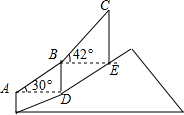 如图,登山缆车从点A出发,途径点B后到达终点C,其中AB段与BC段的运行路程均为200m,且AB段的运行路线与水平面的夹角为30°,BC段的运行路线与水平面的夹角为42°,求缆车从点A运行到点C垂直上升的距离.(参考数据:sin42°≈0.67,cos42°≈0.74,tan42°≈0.90).
如图,登山缆车从点A出发,途径点B后到达终点C,其中AB段与BC段的运行路程均为200m,且AB段的运行路线与水平面的夹角为30°,BC段的运行路线与水平面的夹角为42°,求缆车从点A运行到点C垂直上升的距离.(参考数据:sin42°≈0.67,cos42°≈0.74,tan42°≈0.90). 如图,点F、C在BE上,AB∥DE,∠A=∠D,BF=CE,求证:AB=DE.
如图,点F、C在BE上,AB∥DE,∠A=∠D,BF=CE,求证:AB=DE.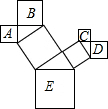 如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形.若正方形A、B、C、D的边长分别是3、4、2、3,则最大正方形E的面积是38.
如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形.若正方形A、B、C、D的边长分别是3、4、2、3,则最大正方形E的面积是38.