题目内容
13.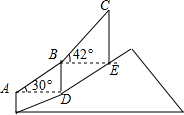 如图,登山缆车从点A出发,途径点B后到达终点C,其中AB段与BC段的运行路程均为200m,且AB段的运行路线与水平面的夹角为30°,BC段的运行路线与水平面的夹角为42°,求缆车从点A运行到点C垂直上升的距离.(参考数据:sin42°≈0.67,cos42°≈0.74,tan42°≈0.90).
如图,登山缆车从点A出发,途径点B后到达终点C,其中AB段与BC段的运行路程均为200m,且AB段的运行路线与水平面的夹角为30°,BC段的运行路线与水平面的夹角为42°,求缆车从点A运行到点C垂直上升的距离.(参考数据:sin42°≈0.67,cos42°≈0.74,tan42°≈0.90).
分析 要求缆车从点A运行到点C的垂直上升的距离,就是求BD+CE的值.解直角△ADB,利用30°角所对的直角边等于斜边的一半得出BD=$\frac{1}{2}$AB=100m,解直角△CEB,根据正弦函数的定义可得CE=BC•sin42°.
解答 解:在直角△ADB中,∵∠ADB=90°,∠BAD=30°,AB=200m,
∴BD=$\frac{1}{2}$AB=100m,
在直角△CEB中,∵∠CEB=90°,∠CBE=42°,CB=200m,
∴CE=BC•sin42°≈200×0.67=134m,
∴BD+CE≈100+134=234m.
答:缆车从点A运行到点C的垂直上升的距离约为234m.
点评 本题考查了解直角三角形的应用-坡度坡角问题,锐角三角函数的定义,结合图形理解题意是解决问题的关键.

练习册系列答案
相关题目
5.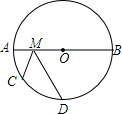 如图,AB是⊙O的直径,AB=8,$\widehat{AB}=2\widehat{AD}$=6$\widehat{AC}$,M是AB上一动点,则CM+DM的最小值( )
如图,AB是⊙O的直径,AB=8,$\widehat{AB}=2\widehat{AD}$=6$\widehat{AC}$,M是AB上一动点,则CM+DM的最小值( )
 如图,AB是⊙O的直径,AB=8,$\widehat{AB}=2\widehat{AD}$=6$\widehat{AC}$,M是AB上一动点,则CM+DM的最小值( )
如图,AB是⊙O的直径,AB=8,$\widehat{AB}=2\widehat{AD}$=6$\widehat{AC}$,M是AB上一动点,则CM+DM的最小值( )| A. | 8 | B. | 6 | C. | 2+2$\sqrt{7}$ | D. | 4$\sqrt{3}$ |
 已知:如图,∠B=∠C=90°,AF=DE,BE=CF.
已知:如图,∠B=∠C=90°,AF=DE,BE=CF. 已知:如图,△ABC中.
已知:如图,△ABC中. 已知:如图⊙O中,直径CD⊥弦AB于E,⊙O的半径为6cm.CE:ED=3:1,求AB的长.
已知:如图⊙O中,直径CD⊥弦AB于E,⊙O的半径为6cm.CE:ED=3:1,求AB的长.
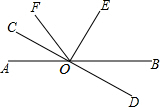 如图,已知直线AB和CD都交于点O,∠COE=90°,且OF平分∠AOE.
如图,已知直线AB和CD都交于点O,∠COE=90°,且OF平分∠AOE.