题目内容
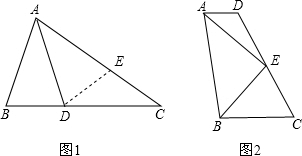
9. 如图,在△ABC中,BD、CE是高,G、F分别是BC、DE的中点,连接GF,求证:GF⊥DE.
如图,在△ABC中,BD、CE是高,G、F分别是BC、DE的中点,连接GF,求证:GF⊥DE.
分析 连接EG、FG,根据直角三角形斜边上的中线等于斜边的一半可得DG=EG=$\frac{1}{2}$BC,再根据等腰三角形三线合一的证明即可.
解答 证明:如图,
连接GE、GD,
∵△ABC中,BD、CE是高,
∴△BEC和△BDC是直角三角形,
∵G是BC的中点,
∴GE=GD=$\frac{1}{2}$BC,
∴△GED是等腰三角形,
∵F是DE的中点,
∴GF⊥DE.
点评 本题考查了直角三角形斜边上的中线等于斜边的一半的性质,等腰三角形三线合一的性质,熟记性质并作出辅助线构造出等腰三角形是解题的关键.

练习册系列答案
相关题目
17.方程4x2=16的解是( )
| A. | x=±4 | B. | x=4 | C. | x=-4 | D. | x=±2 |
19.下列说法正确的是( )
| A. | 所有的等腰三角形都相似 | B. | 有一对锐角相等的两个三角形相似 | ||
| C. | 相似三角形都是全等的 | D. | 所有的等边三角形都相似 |
 画出如图组合体的三种视图.
画出如图组合体的三种视图. 已知:如图,∠B=∠C=90°,AF=DE,BE=CF.
已知:如图,∠B=∠C=90°,AF=DE,BE=CF. 已知:如图,△ABC中.
已知:如图,△ABC中.